Г РИЗОНТ РИЗОНТ
в_о_з_м_о_ж_н_о_г_о_______________________________
[ < ] [ оглавление ] [ > ]
По материалам спора на конференции "Мембраны" 26.01 2005 - 01.02.2005
"Парадокс" межзвездной прямоточки
или
сквозь Бассард-барьер на "бильярдном звездолете"
Зри в корень!
К. Прутков.
Постановка проблемы
Физик Роберт Бассард в 1960-м, предложил следующую идею двигателя. Крайне разряженный межзвездный водород (примерно 1 атом на см3) по курсу корабля можно собирать
в гигантскую магнитную воронку и использовать этот улов как термоядерное горючее в двигателе-реакторе для разгона корабля. Так как в этом случае
мы не ограничены запасами топлива на борту, скорость полета корабля может быть сколь угодно близкой к скорости света с = 300 000 км/с.
Но возникает вопрос.
Пускай при сжигании собранного водорода в гелий выделяется 0.5% энергии покоя (E=0.005mc2). Рассмотрим идеальный случай, когда
вся энергия реакции полностью превращается в упорядоченную кинетическую энергию продуктов реакции в двигателе:
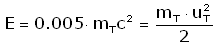
Дефектом массы пренебрежем, так как он незначителен. Но даже в таком идеальном двигателе реактивная струя не может вылетать из его сопла со скоростью большей чем:
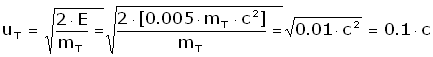 = 30 000 км/с = 30 000 км/с
Это предельно возможная скорость истечения. Корабль Бассарда, отбрасывая килограмм топлива получить импульс ( mTuT ),
больший, чем 30 000 кг.км/с (КН.с) не может.
При этом, собирая тот же килограмм водорода у себя по курсу, судно получит от него тормозящий импульс равный -mTvК, где vК -
текущая скорость корабля.
Пока скорость корабля vК меньше скорости истечения uT = 30 000 км/с, выигрыш в импульсе от
двигателя по сравнению с тормозящим эффектом собирающей воронки есть. Но если корабль уже летит с такой вот предельной скоростью,
то каждый килограмм межзвездного вещества, влетая в ловушку-сборник, будет иметь такой же импульс, как и при сжигании его в двигателе.
Значит, по закону сохранения импульса, сколько бы мы ни жгли водород в реакторе, суммарный импульс (отбрасываемой массы и собираемой)
останется нулевым. А это значит, что преодолеть барьер скорости в 30 000 км/с корабль Бассарда не может.
А если может (как утверждают знающие люди), то где ошибка (что не учтено) в вышеприведенных рассуждениях? Задача в стиле занимательной
физики или "а ну-ка догадайся!"
Бильярдная ракета
Идея: В прямоточке Бассарда газ необязательно тормозить полностью. Магнитное поле может сжимать его "на полном ходу" до начала термоядерной реакции.
Это первая мысль, которая приходит в голову при попытке решить проблему барьера 30 000 км/с. И это неверный ответ. Правильный ответ в другом и он прост. Достаточно выписать пару школьных уравнений и нам все "станет ясно". Мы это обязательно сделаем в конце.
Но не будем исткать "легких" путей. "Нормальные герои всегда идут в обход".
Давайте для начала воспользуемся "американским методом рассуждений". "Американский", он потому что у наших, даже самых лучших
популяризаторов, я такого никогда не встречал, а вот некоторые авторы журнала "Scientific American", в свое время, меня просто купил подобного
рода методами рассуждений! Ставится мысленный эксперимент, который приводит к качественному восприятию сути эффекта. При этом идея
эксперимента бывает настолько "ненормальной", что это даже красиво. Но, правильно упростив реальность, можно получить удивительный результат!
Зримо увидеть суть достаточно сложного эффекта. Я думаю, с задачей о парадоксе Бассард-барьера мы имеем тот самый случай, когда можно это
проделать. Поэтому попробуем.
Назовем наш мысленный эксперимент - "бильярдной ракетой" или "бильярдным звездолетом". Представим себе следующую, доведенную до абсурда схему, имитирующую полет корабля Бассарда. Пускай в космосе по курсу нашего полета, на равном расстоянии друг от друга расположены "бомбы". Они неподвижно висят в вакууме и ждут, когда их подберут. Каждая "бомба" это два шарика массой m, а между ними сжатая и зафиксированная (неважно как) пружина (ее массой пренебрежем) в которой запасена энергия Е. Этакая гантель. Мы можем взять каждую "бомбу", придать ей какое угодно положение, и каким-то образов отпустить пружину. "Детонировать" ее. Тогда шарики разлетятся в разные стороны (и мы можем четко знать куда) друг от друга, каждый, получив половину энергии пружины E/2, а значит
легко узнать их скорость 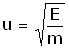
Все очень просто.
Теперь мы можем построить бильярдный реактивный двигатель, работающий на таких "бомбах". Это еще проще. В хвосте ракеты мы должны поставить две пластины друг напротив друга под углом 450 к оси корабля (значить под прямым углом друг к другу). Теперь мы помещаем "бомбу" между этими пластинами (так что бы ось "гантели" перпендикулярна оси ракеты) и снимаем чеку. Пружина срабатывает. Шарики летят в разные стороны но каждый ударившись о свою пластину (450), отлетает от нее под углом 900 (как шар о стенку бильярда) и теперь летят, как и положено "газам" из сопла ракеты в нужном направлении. Такой "биллиардный двигатель" есть очень упрощенная модель реактивного двигателя с идеальным КПД.
Легко вычислить импульс, получаемый от взрыва каждой "бомбы". Он равен 2mu (два же шарика!). Каждый такой "взрыв" добавляет нашему кораблю скорость dv= 2mu/M, где М - масса нашего корабля.
Если наш бильярдный корабль - простая ракета, то М включает в себя массу запасенных на борту бильярдных "бомб".
Но мы говорим о проекте Бастарда. Именно для этого мы разместили в космосе на некотором расстоянии друг от друга "бомбы". Поэтому наш бильярдный звездолет работает так. Подлетая к очередной "гантели", он его захватывает широким раструбом (или еще как - пока это не важно), далее трофей передается в хвост, где "бомба" нужным образом ориентируется и "детонирует" прибавляя кораблю импульс и скорость.
Проблема барьера на бильярдный аналогии выражается вот в чем. Мы стоим на носу корабля и видим как очередная "бомба" подлетает к нам.
Пускай корабль летит со скоростью v. Значит, каждая бомба подлетает к нам со скоростью v несет импульс 2mv, который мы должны погасить, поймав ее. То есть "останавливая" каждую "бомбу" мы принимает ее импульс. Для внешнего наблюдателя (который строил цепочку из бомб, то есть покоится относительно "бомб") конечно же все выглядит иначе. "Бомба", которую мы ловим "на самом деле" покоится, но, столкнувшись с несущейся на нее ракетой, она получила дополнительный импульс 2mv, забрав такое же количество импульса у самой ракеты (ведь закон сохранения импульса работает)
До тех пор, пока v < u, положительный импульс, полученный в результате "взрыва" "бомб" будет перекрывать отрицательный импульс, полученный в результате торможения (разгона "бомб" до скорости корабля). Но как только скорость станет 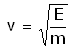 ,
импульсы сравняются и разгон прекратиться. ,
импульсы сравняются и разгон прекратиться.
Теперь самое время рассмотреть высказанную выше идею. Действительно, зачем каждую "бомбу" ловить, то есть разгонять до скорости корабля? Нельзя ли сделать так: "Бомбы" расположены строго на одной оси совпадающей с осью корабля. Для чистоты рассуждений предположим, что каждая "бомба" уже ориентирована как нам надо. Поэтому, пролетая через воронку (на скорости v), она, не задерживаясь, ни с чем не реагируя, быстренек пролетает через весь корабль и оказывается между наклонными пластинами. Тут-то мы ее и детонируем.
Уловили идею? Тормозить (если смотреть с точки зрения экипажа) вернее разгонять топливо, прежде чем его спалить, совсем не обязательно. Его можно сжигать на его собственно скорости.
Но я не зря придумывал эти самые шары, пружины и пластины под углом в 450. Это чтобы рассуждения о энергии покоя, давлении, температуре и прочих сложностях не замаливали нам физически мыслящий глаз! (мозгами люди мыслят плохо, по себе знаю! Глазом - лучше :)
Из приведенной схемы (рис a) видно, что если "бомбы" будут пролетать через ракету на предельной скорости v=u, то в двигателе они просто не сработают!
Взрываться они будут, но ведь "бомба" уже улетает из двигателя со скоростью v. Поэтому разлетающиеся массы просто не догонять наклонные пластины,
чтобы передать им импульс! Как раз скорость v=u это та скорость, при которой шары в нашем двигателе летят параллельно пластинам.
Под углом 450. То есть никакой передачи импульса ракете не произойдет.
"Разумная" мысль "положить" пластины (рис b) тоже на дет результата. Шары ударяться будут, но толку-то? Суммарный импульс от их соударений = 0.
Проще говоря, сам фат, что реактивная струя вылетает из сопла с некоторой скоростью, еще не означает что ракета получает от этой струи
какой-то импульс. Пролетающая сквозняком энергия, никак не участвует в увеличении энергии самой ракеты.
Столкновения с набегающим потоком частиц нам избежать не удастся.
И для того чтобы понять, как же можно преодолеть Бассард-барьер, давайте переместимся на нос корабля. И так, мы на борту корабля,
у горловины воронки. И вот мы видим, как к нам подлетает очередная "бомба". На самом деле это мы к ней подлетаем. Но "на самом деле"
зависит от системы отсчета. Поэтому в нашей системе отсчета "бомба" подлетает к нам, неподвижным, на скорости v. Если мы
ее не будем ловить, то что произойдет? Она ударится о нос корабля и... отлетит от него как бильярдной шар от стенки со скоростью почти
-v. (ведь наш корабль тоже чуть-чуть "отскочит" в противоположную сторону) Произойдет упругое соударение. Верно? (рис. с)
Но мы их ловим. Не даем улететь обратно.
А что это значит (рис d)?
Это значит, что соударение "бомбы" с кораблем - неупругое. Когда они подлетают к нам, мы ловя "бомбы", гасим в нашей
системе отсчета ее скорость. А это значит что "в наших руках выделится" вся кинетическая энергия "бомбы", которую мы ловили. В виде тепла.
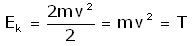
ПОЭТОМУ!
Есть только один способ для бильярдного Бассарда преодолеть барьер скорости u=v. Чтобы иллюстрировать эту идею предположим, что
та самая невесомая пружина хотя и сжата до энергии Е, но при желании может сжиматься еще сильнее и предела этому дополнительному
сжатию мы устанавливать не будем. Другое допущение. Пускай все "бомбы" (они ведь напоминают по форме гантель) расположены продольно курса
корабля.
Теперь если мы подлетаем к "бомбе", то сталкиваясь с ней, мы дополнительно сжимаем уже и без того сжатую пружину. Вот это сжатие, которое мы
успеем получить (пока действует сила инерции подлетевшей бомбы), прежде чем наша бомба разгонится до нашей скорости (с точки зрения внешнего
наблюдателя), и есть дополнительная энергия dE, которая потом должна компенсировать потерю импульса.
Процесс тонкий и сложный. Здесь нужно вовремя вставить чеку! Мы как бы подзаряжаем "бомбу". И чем больше наша скорость, тем больше мы
ее должны подзарядить. И вот теперь, когда мы разрядим все это в сопле, мы высвободим Е+dE. Поэтому шары получать бОльшую
скорость и наш бильярдный Бассард продолжит разгон за пределом скорости u.
Вот воистину "через тернии к звездам!"
* * *
И так, воспользовавшись идеей бильярдной ракеты мы выяснили тонкость, динамики полета корабля Бассарда за пределами скорости 30 000 км/с.
Мы это сделали почти не прибегая к рассуждениям, связанным с термодинамикой.
Но как все это выглядит без шаров, пружин и прочих ухищрений на грани идиотизма?
Если мы выставим впереди несущегося корабля гипотетическое "магнитное зеркало", то здесь произойдет упругое соударение межзвездного
газа с магнитным полем. Частицы ионизированного газа налетая на "магнитное зеркало" с импульсом mv в итоге остановятся, как бы
деформируя магнитную "пружину", а потом отразятся со скорость -mv, обгоняя корабль. Находясь в системе отсчета зеркала (корабля)
мы будем видеть как частицы подлетают к нам с огромной скоростью, останавливаются, и опять улетают от нас. В магнитной воронке корабля
Бассарда мы должны осуществлять только половину этого процесса. Воронка не должна давать частицам улететь. В ней как-то должно быть
организовано неупругое соударение.
В этом - суть.
Если два шара m1 и m2 упруго сталкиваются на скоростях v1 и v2,
а после этого разлетаются со скоростями u1 и u2, то при этом сохраняется не только импульс системы:
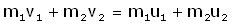
...но и суммарная кинетическая энергия до столкновения шаров равна энергии после их столкновения:
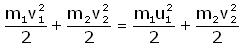
А теперь рассмотрим неупругое столкновение шаров из пластилина.
Столкнувшись, они слипнутся и начнут двигаться вместе. Импульс системы до и после неупругого столкновения ТОЖЕ сохраняется:
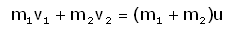
Но если вы теперь из этого уравнения, зная m1,v1 ,m2, v2, высчитает скорость u , а потом подсчитаете кинетическую энергию системы "до" и "после" столкновения то обнаружите, что энергии не хватает:
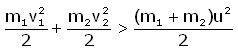
Куда она делась? Говорят: пошла на деформацию пластилина. Но это не совсем правильно. Она превратилась в тепло и рассеялась.
Вот в чем секрет. Если наш прямоточка будет рассеивать энергию неупругого столкновения с частицами, то она никогда не преодолеет барьер.
Представьте себе несущийся в межзвездном пространстве корабль Бассарда. Водород попадает в воронку. Он ударяется об нее и должен отлететь
с почти удвоенной скоростью от корабля (корабль имеющий массу ориентировочно 10 000 тонн почти не чувствует импульс килограмма водорода,
а тот отскакивает от него как горох от стенки). То есть воронка будет формировать струю водорода перед кораблем и ничего не улавливать.
А чтобы этого не произошло, надо удерживать отскакивающий водород. Нужно организовать для него неупругое соударение. Какой бы механизм
удержания водорода мы не избрали, в итоге энергия собранного воронкой газа (в системе отсчета корабля) превратится в тепло
(и надо сказать очень большое). Что бы преодолеть барьер скорости это тепло нужно рекуперировать, то есть опять
(с термодинамическими потерями, конечно) превратить в реактивную струю с нужным направлением импульса (то есть получить из этого тепла работу).
Так сказать, транслировать или передать на выход, эту кинетическую энергию транзитом. А термодинамические потери на тепловой КПД двигателя
придется компенсировать за счет извлечения термоядерной энергии синтеза и еще иметь чуть-чуть сверху. Вот это "чуть-чуть сверху" и будет
по идее разгонять корабль за пределом барьера в 30 000 км/с.
Но учитывая термодинамические сложности связанные с преобразованием...
Кинетическая энергия --> Тепло --> Кинетическая энергия
... и то что с ростом скорости будет расти и температура (а значит энтропия газа, а значить падать тепловой кпд системы), то термодинамические
потери будут расти и "чуть-чуть" будет все меньше и меньше. Вполне возможно, что очень скоро дань второму началу термодинамики съест все то, что вырабатывает термоядерный реактор и Бассард упрется в очередной "барьер".
Хотя теоретически мы имеем выигрыш, и можем бесконечно долго разгонять нашу прямотоку, практически задача оказывается почти безнадежной.
В общем, не благодарная это инженерная задача - лететь на корабле Бассарда к звездам. Термодинамика встает на пути реализации этого проекта
стеной.
Еще один вариант прямоточного привода.
Коль мы пользуемся "американским" методом, интересно описать с его помощью принцип действия двигателя, о котором в процессе дискуссии рассказал Валентин Подвысоцкий. Назовем ее "безреакторная прямоточка":
"Захваченное вещество попадает внутрь двигателя. В результате его торможения, выделяется энергия. Часть этой энергии, тем или иным образом, может быть использована для ускорения бортовых запасов реактивной массы. "
То есть, такая прямоточка не использует никакого источника энергии. Она ее вырабатывает в результате торможения собираемого в воронку газа. За счет его торможения. И сам корабль при этом... ускоряется! Как не парадоксально, но такой двигатель физически вполне реалистичен, хотя расплата за эту необычность будет очень жестокой.
Но давайте по порядку.
Как смоделировать такой двигатель в нашей бильярдной аналогии?
Смотрите. По курсу ракеты расположены уже не "бомбы", а просто шары массой m. Кроме того, на борту корабля у нас есть запас таких же шаров, тоже массой m. Но, к каждому приделана та самая волшебная невесомая пружина, которая теперь у нас разжата. Никаких внутренних запасов энергии у нас нет. Как теперь мы действуем?
Стоя на носу ракеты мы держим очередной шар из запасника, выставив разжатую пружину вперед. Вот мы видим: подлетает очередной внешний шар. Наша задача - поймать его в неупругом соударении. Вот подлетающий шар ударяется о выставленную нами пружину, специальный замок захватывает его и он начинает тормозить свою скорость за счет сжатия пружины. Вот шар остановился (конечно это для наблюдателя на борту корабля). За миг до того как он должен отскочить (пружина разжаться) мы вставляем чеку.
В результате у нас в руках появилась новая "бомба". Где взялась энергия для нее? Это та энергия которая должна была рассеивается в процессе неупругого соударения. Помните?
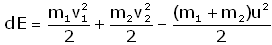
А за счет чего появляется дополнительный импульс у всей нашей ракетной системы? За счет массы запасенной на борту. Ведь в воронку-заборник влетел один шар, а через двигатель мы выкинем два.
Давайте подсчитаем.
Пусть мы летим на корабле массой 10 кг со скоростью 2 м/с и ловим шар весом 1 кг. Его импульс 0. Наш mv = 20. После неупругого столкновения получается, что корабль стал весить 11 кг и теперь летит с несколько меньшей скоростью 1.81818... м/с
Но "энергия деформации неупругого соударения" уже запасена в пружине. Она равна 2 Дж (будем уточнять почему?). И теперь если мы израсходуем ее на разгон двух шаров массой по 1 кг то получим для них скорость 1,4142... (корень из двух. Тоже, думаю, объяснять не надо). Значит импульс отбрасываемой массы 2 x 1,4142... =2,828427... Этот же импульс получит и ракета, которая полегчала на два шара и теперь весит 9 кг. Значит прирост ее собственной скорости 0,31427...
Но мы же потеряли в скорости, когда ловили шар на входе. Поэтому в итоге мы имеем в сумме скорость: 1.81818...+ 0,31427... = 2,13245... А перед тем как поймать шар - имели 2 м/с.
То есть, потеряв килограмм собственного топлива, мы выиграли 0.13234... м/с. Это 6.6% от скорости. И с увеличением скорости корабля, прирост скорости будет один и тот же 6.6%! Относительный прирост скорости не зависит от прочих параметров. Теряя 10% массы, вы выигрываете 6.6% от уже достигнутой скорости.
Не густо, если учесть что мы собираемся достигнуть скорость хотя бы 20000 км/с.
Такой корабль, как и обычная ракета является телом переменной массы. То есть обе расходуют запасенную на борту массу. Давайте сравним обе схемы качественно.
Вот смотрите. Допустим, мы уже летим на предельной скорости. Возьмем знаменитые 30 000 км/с (установленный нами теоретический барьер для Бассарда). Теоретическая скорость истечения из безреакторной прямотоки на такой скорости будет не больше 30 000 км/с (то есть предельной для продуктов термоядерного синтеза). А до этого она была еще меньшей!!!
А ведь классическая термоядерная ракета в этом смысле выглядит куда лучше! У нее предельная скорость истечения (теоретически) с самого начала 30 000 км/c.
А это значит, что соотношение масса топлива/ масса полезной нагрузки в случае безреакторной прямоточки ГАРАНТИРОВАННО будет много хуже чем у "простой" ракеты сжигающей термоядерное горючее и выбрасывающее его с максимальной скоростью с самого момента старта.
А учитывая, что создание захватывающей воронки с хорошей рекуперацией тепловой энергии, куда большая проблема, чем создании термоядерной ракеты, то вообще становится ясно - овчинка не стоит выделки.
Но совсем выкидывать идею не стоит. Кто знает? В некоторых экзотических случаях схема может оказаться вполне работоспособной и даже очень выгодной. Первая мысль- использовать как последнюю ступень при разгоне. Но самая здравая - как усилитель электромагнитного тормоза.
Александр Семенов
___________________________________________
[ < ] [ вверх ] [ оглавление ] [ > ]

Оптимизирован под Internet Explorer 1024X768
средний размер шрифта
Дизайн A Semenov
|