Анализ поведения плазмы в магнитном сопле представляет интерес для проектирования ракеты, тяга которой создается продуктами инерционного термоядерного синтеза инициируемого лазерами. В магнитном сопле можно достигнуть высокой скорости истечения (высокой эффективности использования массы отбрасываемого топлива), потому что в процессе истечения из двигателя плазма не вступает в прямой контакт со структурой, формирующее камеру сгорания. Некоторые концептуальные решения для ракеты на лазерном термоядерном синтезе (laser fusion rocket LFR) были предложены. Ракета оборудована магнитным соплом который формирует направленную струю плазмы, возникшую в результате инерционного лазерного синтеза, используя для этого сверхпроводящую (superconducting magnetic SCM) катушку ("витка" или "контура"), которая и принимает импульс от расширяющейся плазмы.
Гайд (Hyde) разработал LRF и предложил магнитное сопло, использующее два SCM витка. Потом он предложил новый проект и оценил эффективность тяги, используя для этого двумерную (2D) магнитогидродинамическую (magnetrohydrodynamics MHD) вычислительную модель для одного витка. Как утверждалось, эффективность тяги в этом случае составила 65%. Нагамине и Накашима (Nagamine and Nakashima) рассчитали поведение плазмы и эффективность тяги используя трехмерную (3D) гибридную вычислительную модель для магнитного сопла, использующего одну магнитную катушку и исследовали как изменяется эффективность тяги при изменении некоторых параметров. Так как эти оценки были выполнены для магнитного сопла с одной катушкой, мы исследовали поведение плазмы и эффективность тяги, используя трехмерный гибридный код для модели с двумя катушками и оценили возможность оптимизации эффективности такого сопла.
Эффективность тяги n ("ню") определялась в терминах импульса следующим образом:

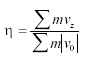
Где m масса иона v_z - проекция скорости иона на ось Z, |v₀|- абсолютное значение начальной скорости иона. Сумма (сигма) производится для всех частиц плазмы. Следовательно, наша задача - увеличить +Z компоненту скорости ионов плазмы, как показано выше.

2. Вычислительная модель

Для моделирования поведения плазмы в магнитном сопле мы разработали 3D гибридный код (программу) на основе модели предложенной Хоровичем (Horowitz). Программа моделирует ионы как индивидуальные частицы, а электроны как жидкость. Этот подход допустим, если поведение системы хорошо описывается физикой ионов. Принятая нами для вычислений схема приведена на рис. 1. Она основана на модели Нагамине (Nagamine's) к которой добавлена задняя катушка (rear coil) (R) для повышения эффективности тяги.

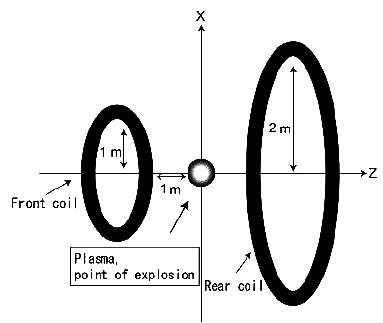
рис. 1 Схема вычислительной модели.

Параметры для катушки R выбраны пропорциональным понижением параметров принятых Гайдом (Hyde). Положение катушки R изменялось от -2 до +3 м. Ток в заднем витке изменялся от 0.595 до 2.38 MA. Ток переднего контура фиксированный и составлял 3.57MA. Начальная форма плазмы принималась в виде шара fp радиусом 0.3 м и представляет собой ионы золота общей массой 110 миллиграмм. Начальная кинетическая энергия плазмы принята в 4 MДж и электронная температура 0 эВ. Отношение кинетической энергии плазмы и энергии поля - обычно 0.1. В данном случае энергия поля - суммарная энергия двух катушек. Другие параметры вычислительной модели те же самые, что и в модели Нагамине и Накашима (Nagamine and Nakashima).

3. Результаты и выводы

Результаты вычислительной модели показаны на рис 2 как функция от положения задней катушки R (Z) и тока в ней (I).

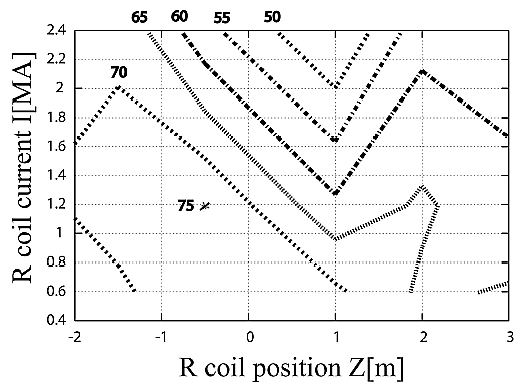
Рис. 2 Эффективность тяги (%) как функция от Z - положения (в метрах) и тока во втором контуре I (мега-Амперах)

Максимальная эффективности тяги составила 75% для Z = -0.5 м и I = 1.19 MA. Размещение контура R в Z=+1.0 м снижало эффективность тяги.
Рис 3 иллюстрирует общую картину распределения векторов скоростей частиц в проекции на ось ХZ через 8 миллисекунд.

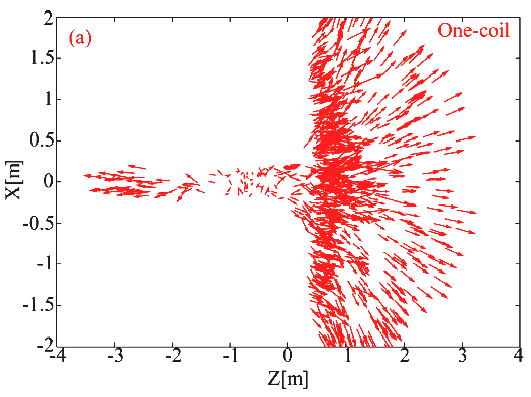
Рис 3.a. Распределение векторов скоростей в проекции на плоскость ХZ: вариант один контур, передний.

Схема на Рис 3.а показывает направление векторов для случая одного контура.

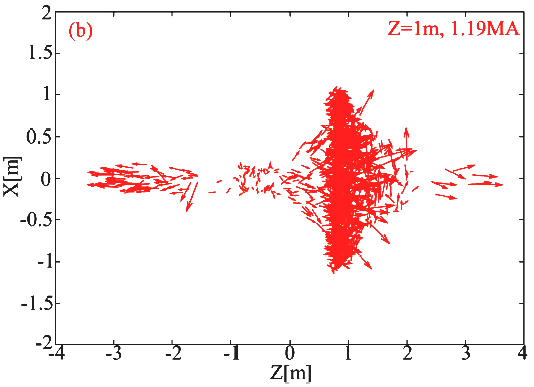
Рис 3.b Распределение векторов скоростей в проекции на плоскость ХZ: вариант два контура. Z= +1.0 I = 1.19 MA

Схема на рис. 3.b демонстрирует общее направление векторов скоростей для случая Z= +1.0 м и тока I = 1.19 MA.

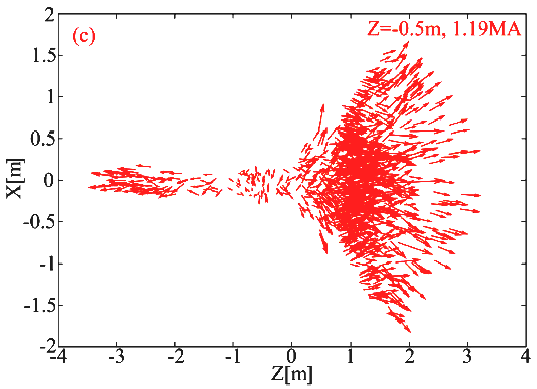
Рис. 3.с Распределение векторов скоростей в проекции на плоскость ХZ: вариант два контура. Z= -0.5 I = 1.19 MA

Схема на рис. 3.с демонстрирует картину векторов скоростей для случая Z= -0.5 м и тока I = 1.19 MA, соответственно. Хотя нам кажется, что именно в случае b очень много частиц, изотропно расширяющейся плазмы, направлены (коллимируются) в направлении +Z, но здесь эффективность составляет всего 61%. Ниже, чем в случае с - 75%.
Рисунок 4 показывает распределение напряженности магнитного поля в начальный момент (инициализации) и через 0.5 миллисекунд после, для случая Z=-0.5 m и I=1.19 MA. Магнитное поле выталкивается из района занятого плазмой и видно, что оно через 0.5 мс сжимается, чтобы сработать как отбрасывавшая пружина для плазмы. Подобная картина наблюдается и для всех остальных случаев.

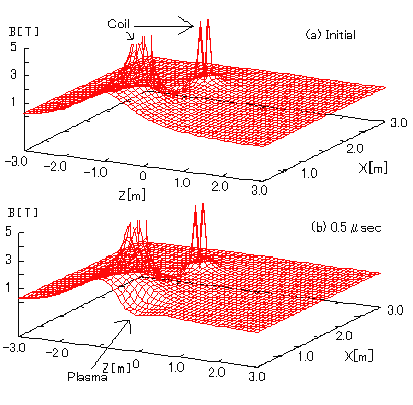
Рис. 4 Распределение магнитного поля (а) в момент инициализации (b) через 0.5 миллисекунды.Вариант Z= -0.5 I = 1.19 MA

Рисунок 5 показывает распределение скоростей ионов плазмы по составляющей vz через 8 миллисекунд для одноконтурного случая (рис. 5.а); случая с двумя контурами и Z=+1.0 m (рис. 5.b); случая с двумя контурами и Z=-0.5 m (рис. 5.c).
На рисунке 5.а видно две скоростных компонента в районе Z= +1.0 m. Это указывает на то, что дополнительный контура R размещенный в этом месте - сильно повредит.

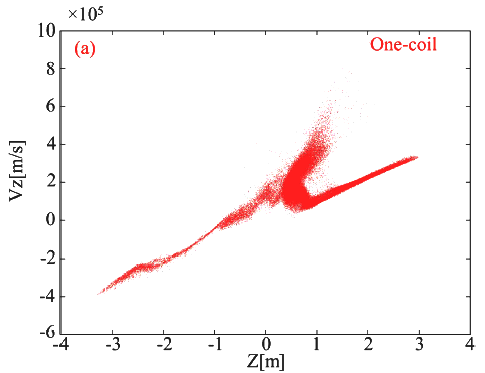
Рис. 5.a Распределение v_z. Вариант один контур, передний.

Рисунок 5 b показывает, что более низкий компонент скорости замедлен по сравнению со случаем а.

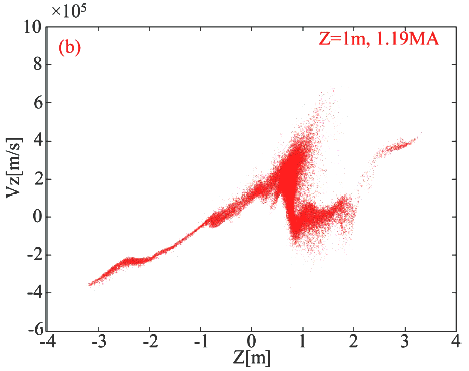
Рис. 5.b Распределение v_z. Вариант два контура. Z= +1.0 I = 1.19 MA

С другой стороны рисунок 5.с показывает, что менее скоростной компонент, теперь наоборот ускорен, потому что вторая катушка перемещена в Z= -0.5 m.

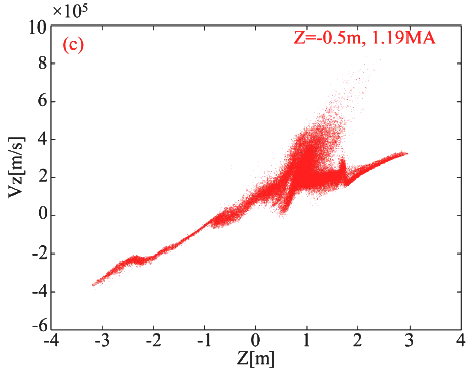
Рис. 5.с Распределение v_z. Вариант два контура. Z= -0.5 I = 1.19 MA

Это объясняет, почему мы получаем более низкую эффективность для случая b.

За увеличение эффективности тяги, достигнутое использованием двух катушек, придется расплачиваться увеличением массы системы в связи с использованием дополнительного контура, лучевого экрана для них и дополнительных радиаторов для рассеивания излишков тепла. Предварительная оценка по уравнениям, используемым Гайдом (Hyde) для массы системы, показывает, что системе из двух потребуется повышение эффективности тяги более чем до 73% чтобы выиграть у одновитковой системы той же мощности по отношению эффективности, определенной как отношение эффективности тяги к массе конструкции.

4. Заключение

LFR использует магнитное сопло для формирования из изотропно расширяющейся плазмы направленный поток. Вычислительное моделирование эффективности для магнитного сопла, использующего два витка, производилось на 3-D гибридном коде. Максимальная эффективность достигла 75% по сравнению с 65% полученными для одновитковой схемы. Было так же обнаружено что размещение второй (задней) катушки
в позиции +Z уменьшает эффективность из-за того, что поле этого контура будет тормозить частицы плазмы.

References:

[1] Hyde, R. A., Wood Jr, L. L., Nuckolls. J. H.: Prospects for Rocket Propulsion with
Laser-induced Fusion Microexplosions, AIAA Paper, No.72-1063, 1972
[2] Hyde, R. A.: A Laser Fusion Rocket for Interplanetary Propulsion, Lawrence
Berkeley Laboratory, UCRL-88857, 1983
[3] Nagamine, Y., Nakashima, H.: Analysis of Plasma Behavior in a Magnetic Thrust
Chamber of a Laser Fusion Rocket, Fusion Technology, Vol. 35, pp.62-70, 1999
[4] Horowitz, E. J., Schumaker, D. E., Anderson, D. V.: QN3D: A Three-Dimensional
Quasi-neutral Hybrid Particle-in-Cell Code with Applications to the Tilt Mode
Instability in Field Reserved Configurations, J. Comp. Phys., Vol.84, pp. 279-310, 1989

Перевод: Александр Семенов. Ноябрь, 2007 г.

Первоисточник:
Thrust Efficiency Calculation for Magnetic Nozzle in Laser Fusion Rocket
N. Sakaguchi, Y. Kajimura, H. Nakashima
Trans. Jpn. Society for Aeronautical and Space Sciences, Vol.48, No. 161, pp.180-182(2005)

Скачать PDF-файл на английском. __________________________________________________ [ вверх ] [ оглавление ]

Оптимизирован под Internet Explorer 1024X768
средний размер шрифта
Дизайн A Semenov