Г РИЗОНТ РИЗОНТ
в_о_з_м_о_ж_н_о_г_о______________________________________
[ оглавление ]
Laser-powered Interstellar Probe
Geoffrey A. Landis
The Text portion of the presentation made at the Conference on Practical Robotic Interstellar Flight, NY University, New York, NY Aug. 29-Sept. 1, 1994.

|
Межзвездный ионный зонд,
снабжаемый энергией
по лазерному лучу
Джеффри А. Лэндис
1994 г.
|
П р е з е н т а ц и я
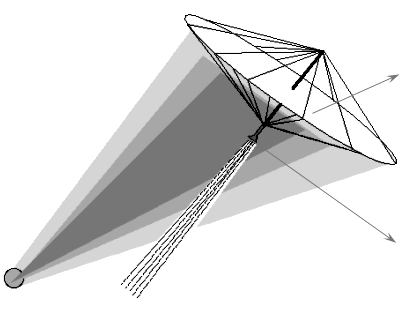 Межзвездный зонд, снабжаемый энергией по лазерному лучу (схема)
Межзвездный зонд, снабжаемый энергией по лазерному лучу (схема)
|

солнечные батареи

ионный двигатель
|
Неподвижный лазер (слева) освещает светом массив солнечных батарей, показанный как натянутая центробежной силой мембрана с тонкой сеткой проводов. По ним собирается фотоэлектрический ток. Полученная таким образом энергия питает ионный двигатель.
Далее представлена текстовая часть презентации, сделанной на конференции по автоматическому межзвездному полету (Conference on Practical Robotic Interstellar Flight) в Нью-Йоркском университете проходившей с 29 августа по 1 сентября 1994 г.
Проблема: необходимо добиться максимальной эффективности использования энергии ракетой.
Эффективность определяется как дельта-V достигнутая на килограмм отброшенной массы за киловатт полученной энергии.
Максимальная энергетическая эффективность не совпадает с максимальным импульсом.
Максимальная энергетическая эффективность ракеты достигается, если скорость истечения рабочей массы в любой момент разгона равна мгновенной скорости корабля.
Ve=V
Почему? 100% энергетическая эффективность будет достигнута тогда, когда затраченная на разгон корабля энергия Е будет равна кинетической энергии корабля: mkvk2/2. И этого можно добиться, если в любой момент разгона скорость отбрасываемой массы равна мгновенной скорости корабля. В этом случае получается, что вся отбрасываемая кораблем масса покоится в системе отсчета старта. То есть ее кинетическая энергия = 0. Корабль как бы вскарабкивается по столбу реактивной массы.
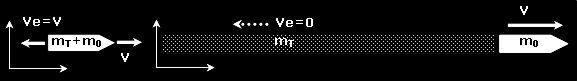
А если реактивная масса стоит "на месте" (это идеализация и тепловым движением пренебрегаем), то это означает что 100% выделившейся в двигателе энергии Е пошло на разгон корабля и только его. Но если в начальный момент скорость корабля близка к 0, то и скорость отбрасываемой массы близка к 0. В идеальном случае мы получаем бесконечное массовое число M (отношение начальной массы ракеты к конечной). Идеальная энергетически ракета невозможна из-за бесконечной стартовой массы. Поправить ситуацию легко. Реальная ракета должна уже иметь некую начальную скорость Vн. Тогда по окончанию разгона и столб отброшенной массы будет иметь эту начальную скорость Vн, а не 0. Его энергия mTVн2/2 - дополнительный расход энергоресурса, и это будет "плата" за здравую стартовую массу. Такая плата незначительно снизит энергетическую эффективность (на доли процента), но позволит говорить о разумном значении числа М.
Тот факт, что "столб всей отброшенной материи" после выключения двигателя имеет одну скорость, позволяет для расчета такой ракеты использовать простейший "школьный" принцип сохранения импульса к которому Лэндис прибегает ниже.
(Серым цветом здесь и ниже - примечания переводчика).
Требуемое массовое отношение
Для случая, когда скорость истечения Ve = мгновенной скорости судна, массовое отношение будет равно бесконечности, если экспедиция стартует с нулевой скоростью!
Очевидно, что такой подход непрактичен, если миссия начинается на скорости, отличной от нуля.
По закону сохранения импульса:
mfvf = mivi
Предположим, что миссия изначально имеет скорость Vi = 30 км/с (это 10-4 от скорости света-с) составляющая, например, скорость в перигелии околосолнечной орбиты. В этом случае массовое отношение будет:
mi/mf = vf/vi=0.11/10-4=1100
Требуемая масса топлива в 1100 раз больше чем масса пустого корабля.
Для сравнения, полезная нагрузка ракеты-носителя Сатурн-V для лунной мисси "Аполлон" составляла, грубо 1% от начальной массы корабля.
Большинство ракетных систем не способны произвольно изменять скорость истечения, чтобы настраивать в полете величину своего удельного импульса. (обычно при запуске на орбиту используются стартовые ускорители - бустеры, что в некоторой мере осуществляет эту идею. То есть первая ступень имеют меньший удельный импульс, чем последующие.)
Поэтому интересен случай энергетической оптимизации скорости истечения, из предположения того, что скорость истечения будет постоянной. Результат такого анализа показывает, что в этом случае эффективность использования по сравнению с ракетой постоянно меняющей скорость истечения, будет на 50% хуже.
Постоянная скорость истечения
(это наиболее вероятный вариант, в сравнении с ракетой, истечение у которой пропорционально мгновенной скорости полета).
Для максимизации энергетической эффективности скорость истечения должна быть ve =2/3 от конечной скорости корабля.
При такой скорости истечения массовое число для судна =4.92
то есть масса топлива 3.92 раза больше чем масса пустого корабля
Конечная кинетическая энергия корабля составит (9/4)/3.92 = 57% от затраченной на разгон энергии.
Эффективность требует платы! Улучшение массового отношения в 200 раз (с 1000 до 5) приводит к уменьшению энергетической эффективности в 2 раза!
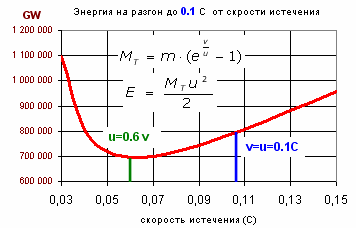 Давайте посмотрим, как Лэндис получил этот оптимум в 2/3. Кинетическая энергия E всей отбрасываемой массы растет, как квадрат скорости истечения u (мы используем классическую механику) и пропорционально запасенной на борту реактивной массе. Но сам запас отбрасываемой массы MT экспоненциально уменьшается с ростом скорости истечения (а значит и общее количество энергии сообщенного всей отбрасываемой массе снижается тоже). В итоге оказывается, что у кривой удельных энергозатрат существует минимум, и на графике видно, что он наступает при Ve ~ 0.6 V.
Давайте посмотрим, как Лэндис получил этот оптимум в 2/3. Кинетическая энергия E всей отбрасываемой массы растет, как квадрат скорости истечения u (мы используем классическую механику) и пропорционально запасенной на борту реактивной массе. Но сам запас отбрасываемой массы MT экспоненциально уменьшается с ростом скорости истечения (а значит и общее количество энергии сообщенного всей отбрасываемой массе снижается тоже). В итоге оказывается, что у кривой удельных энергозатрат существует минимум, и на графике видно, что он наступает при Ve ~ 0.6 V.
То есть при 2/3Vк. Теперь несложно определить и массовое число для ракеты с такой скоростью истечения, и необходимую энергию, и эффективность в сравнении с идеалом. У Лэндиса последний параметр получился 57%, а у меня упорно получается 64%. Потому, что у него массовое число при ve=2v/3 получилось 4.92, а у меня получается 4.48, и как оно мажет быть другим (не e3/2) для меня осталось загадкой.
Предварительная оценка:
Эффективность солнечных батарей 60%
Эффективность лазерного коллектора 85% (первый нуль в дифракционном кольце)
Эффективность двигателя (ионного) 80%
Потеря за счет красного доплеровского смещения 5%
Дополнительный импульс, полученный от поглощения коллектором как световым парусом 9% (об этом см. расчеты в приложении )
В итоге: 24% поступившей по лазерному лучу энергии преобразовано в кинетическую энергию зонда.
Таким образом, лазер должен послать в 4.15 раз больше энергии, чем приобретет к концу разгона зонд.
Для миссии со скоростью 0.11с (Флай-бай Форварда) энергия зонда составляет: 5x1015 Дж на кг. (17 МВт-год/кг),
Значит, необходима лазерная мощность 70 МВт-год/кг
Параметры паруса-коллектора
При принятии ограничения максимальной плотности энергии в луче 16,5 КВт/м2 дабы поддержать низкую температуру коллектора (что потребуется для эффективной работы солнечных батарей) их массив должен иметь минимальную площадь 2.2 км2 (1.7 км в диаметре).
Это может быть либо тонкопленочная батарея диаметром 1.7 км, либо еще большее по диаметру зеркало должно фокусировать поступающий свет лазера на батарею диаметром 1.7 км.
Предположим, мы используем GaInP2 батареи толщиной в 1000 нм. При плотности 4.44 г/см3 (444 кг/м3) 2.2 км2 фотопреобразовательных батарей будут иметь массу 1000 кг.
Приняв 270 кг полезной нагрузки, как предположил Форвард (1989), и предположивт том же самый структурный параметре: массы силовой конструкции =70% от массы паруса (в нашем случае батареи фотопреобразователей), полная масса зонда будет 1970 кг (сравните с 1000 кг принятых Форвардом для своего зонда-паруса в 1989 г.)
Если диаметр фокусирующей линзы такой же, как и для разгоняемого лазером светового паруса, то есть 1000 км, то для длины волны (лямбда) = 670 нм наш зонд получает то же дифракционное ограничение дистанции разгона:
d=2.44 Lambda/D
Это 0.11 св. года - максимальная дистанция разгона. Сравните с 0.17 св. лет для большего по размеру светового паруса. Однако так как ускорение в начале разгона у нашего типа зонда небольшое, а в конце увеличивается в 4.5 раза - то дистанция разгона не представляется здесь большой проблемой.
Сравнение лазерного ионного зонда
с лазерно-световым парусом
1000 кг разгоняемый лазерным лучом зонд-парус требует 65 ГВт-ную мощность лазерного луча в течении 3-х лет разгона (200 ГВт-лет энергии)
Такой же самый исследователь на ионном двигателе с внешним лазерным энергоснабжением потребует 46,3 ГВт-ного луча в течении тех же 3-х лет (138 ГВт-лет энергии)
Ионный вариант уменьшает необходимую мощность с 65 до 46 ГВт, улучшая этот показатель приблизительно в 1.5 раза по сравнению с лазерным парусом.
И все же, в чем достоинство концепции?
1. Можно уменьшить длину волны, используя более широкую запрещенную зону в полупроводнике. Это увеличит монохроматическую эффективность, уменьшит температурный коэффициент и таким образом увеличит допустимую плотность потока энергии и позволит использовать меньшую линзу. Например, зона Eg = 2.26 ЭВ, позволила бы испльзвать длину волны 550 нм, что уменьшило бы линзу до 820 км в диаметре и увеличила эффективность преобразования энергии, грубо до 75%.
Такие изменения снизили бы потребляемую мощность до 38 ГВт.
2. В отличии от лазерного паруса, ионной ракете на лазерном луче безразлично с какой стороны направлена на нее энергия. Она может быть направлена по направлению траектории ее разгона, сбоку или даже против. Если лазерная ионная ракета начнет свой разгон, предварительно удалившись от источника энергии на 0.11 св. лет (таким образом, сначала приближаясь к фокусирующей системе, пройдет мимо и начнет удаляясь от нее) то дистанция разгона может быть удвоена. В итоге необходимую мощность можно разделить на два (хотя в этом случае ионный зонд предварительно придется поместить на 0.11 световых лет от Солнца, а затраченную на это энергию и время надо учитывать тоже).
Удвоение дистанции разгона уменьшит необходимую мощность до 18 ГВт.
Обратите внимание. 9%-ное приращение за счет светового давления от поглощения и отражения луча нужно вычитать в первой половине разгона из общего импульса, а потом, после прохождения "точки рандеву", добавлять.
Технология фотоэлементов
Технология светового коллектора потребует для сверхтонких световых фотопреобразователей получения тех же значений эффективности, что сейчас можно получить для "толстых" моно-кристаллических солнечных батарей. Пока же возможны как высокоэффективные фотопреобразователи, так тонкие пленочные фотоэлементы, но соединение обоих достоинств - серьезный технический вызов. 1.85 ЭВ GaInP2 солнечные батареи уже сегодня доступно и обеспечивают высокую эффективность фотопреобразования. Но полупроводники с более широкой запрещенной зоной станут доступными в будущем.
Фотоэлементы, освещенные монохромным (лазерным) светом могут достигать большей эффективности, чем освещенные широкополосным солнечным светом. Рекуперация лазерного луча с 55% ой эффективностью уже демонстрировалась в лабораторных условиях и достижение 60%-ой эффективности будет не очень сложной задачей для преобразователей с широкой запретной зоной.
Рабочий поток в 16.5 КВт/м2 (примерно в 12 раз мощней чем Солнечная постоянная) не должен представлять проблему для фотоэлементов с такой запретной зоной. Принятая эффективность в 60% означает, что меньшая часть света будет превращаться в тепло, а более широкая зона, большая разность потенциалов означает, что температурный коэффициент для фотопреобразователя будет сравнительно низкий. Однако рабочая температура все же будет высокой, и это может создать проблемы.
Трудности
Мы пренебрегли массой подсистемы электропреобразования и массой двигателя. Но эти массы могут оказаться значительными, и вероятно сделают идею намного менее привлекательной.
Энергетическая подсистема должна собрать и преобразовать 40 ГВт энергии.
Ионный двигатель должен обеспечивать скорость истечения в 0.073 с (удельный импульс 2 миллиона секунд) при тяге в 1570 Н (350 фунтов).
Если реактивная масса - ионизированный водород, то на сетках ионного двигателя для разгона до нужной скорости истечения потребуется разность потенциалов 2.5 МВ.
Такие параметры - вне пределов современной технологии. Даже если трансляция энергии станет возможной при этом без значительного увеличения массы, если и "разумная" масса ионного двигателя будет возможна, идея электроракетного пути решения проблемы запуска межзвездной миссии смотрится все равно менее привлекательной.
Вопрос: существует физическое ограничение на уменьшение массы ионного двигателя? Может ли быть изготовлен ультра-легкий ионный двигатель?
Даже если эти проблемы окажутся сегодня решены, паралинза диаметром 1000 км находится за пределами современных технологических возможностей.
Паралинзу можно было бы сделать много меньшего диаметра. Вместо одной линзы в 1000 км использовать десять по 100 км.
(см. Лэндис 1989 обсуждение)
Гибридные и многоступенчатые конструкции
Ионный привод, снабжаемый по лазерному лучу, и световой парус, разгоняемы давлением луча, не должны рассматриваться как взаимоисключающие альтернативы. Опираясь на выше изложенные соображения об энергетической эффективности, можно предположить, что используя на первоначальной стадии разгона ионный привод, а на конечной парус, можно добиться большей эффективности чем при использовании каждой концепции в отдельности. Обе концепции "парусов" могли бы быть разработаны так чтобы усиливать достоинста друг друга, достигая эффекта синергизма. Например, большой отражающий парус мог бы концентрировать свет на меньшую фотопанель с преобразователями высокой эффективности.
Однако остается неясным, будет ли полученный выигрыш эффективности стоить неизбежной платы за увеличение технической сложности?
Заключение
Опираясь на несколько оптимистические допущения параметров, обсуждавшиеся выше, питаемая внешним лазером электроракета вполне осуществима для запуска межзвездного зонда, и потенциально слегка лучше разгоняемого лазером паруса.
И так:
Практический автоматизированный межзвездный полет,
готовы ли мы к нему сейчас?
Пока нет.
Ионная ракета, снабжаемая энергией по лазерному лучу - заманчивая концепция
но
. . . неосуществима в ближайшее время из-за массы лазерного драйвера и диаметра линзы.
Приложение
Влияние эффекта светового давления (паруса) на коллектора фотоэлементов.
Сила, оказываемая на судно, 187 Н
Световое давление на массив фотопреобразователей будет 1 Н на 3.3 ГВт световой энергии (это половина силы, давящей на зеркальный парус, так как свет только поглощается, но не отражается).
Сила светового давления вносит дополнительные 9% тяги.
Необходимая мощность уменьшается на 9%
Фактически, массовое число с учетом эффекта светового паруса уменьшается до 4.5
Ионная ракета, снабжаемая энергией по лазерному лучу имеет еще одно дополнительное преимущество перед лазерным парусом. Эта методика годится как для разгона, так и для торможения зонда у цели. Но в случае торможения, следует учитывать 9% уменьшение удельного импульса за счет "парусности" судна.
* * *
Перевод, комментарии, оформление А. Семенов, май 2008 г.
Первоисточник
Page by Geoffrey A. Landis 1998
__________________________________________________
[ вверх ] [ оглавление ]

Оптимизирован под Internet Explorer 1024X768
средний размер шрифта
Дизайн A Semenov
|