Г РИЗОНТ РИЗОНТ
в_о_з_м_о_ж_н_о_г_о______________________________________
[ оглавление ]

|
Под парусом в протонном ветре
Исследование принципа магнитного паруса
|
Чарлз Дэнфорт
Университет Джона Хопкинса, Балтимора.
1997 (?) г.
Sailing the Proton Winds
An Investigation into the Principles of Magnetic Sailing
Charles Danforth
Johns Hopkins University, Baltimore, MD 21218
Магнитный парус, ассоциируется с более знакомым всем солнечным парусом тем, что он тоже использует свободную энергию из космического пространства. Солнечный парус использует фотоны, а магнитный парус - заряженные частицы. При этом он может работать в двух режимах с довольно разным результатом. В этой работе предложен проект магнитного паруса и вычислительно смоделировано его поведение, что позволило оценить ожидаемую суммарную тягу. Рассмотрены преимущества и недостатки подобной системы, а также выдвинуты некоторые интригующие перспективы.
1 Введение
Идея плаванья на яхте под парусом и полет на ракете к Марсу редко как-то ассоциируются. В данном случае, однако, интуиция ошибается, так как действительно можно прийти под парусом на Марс или еще куда-нибудь в космосе.
Имеется несколько способов это сделать. Первый - световой парус, хорошо известен любителям фантастики и изобретателям экзотических космических систем. Точно так же как парус на морском судне использует ветер, для перемещения в некотором направлении, так и световой парус использует давление света от Солнца или лазера чтобы создать тягу в противоположном направлении. Обычно такой парус колоссальных размеров лист тончайшей металлической зеркальной фольги в более чем тысячи квадратных метров, накапливающий жиденький импульс отражающихся от него фотонов. Хотя до сегодняшнего момента испытана всего одна маленькая модель, такого рода системы хорошо поняты и очень подробно обсуждаются в других работах. Здесь солнечный парус фигурирует только для сравнения.
Иной способ плавать под парусами в космосе - магнитный парус. Вместо светового давления, магнитный парус в процессе полета разгоняется, воспринимая импульс заряженных частиц.
Схема магнитного паруса очень проста и фактически может быть приспособлена для любого космического корабля уже сейчас. Все что необходимо - электрический провод, токовая петля. Космический аппарат просто выбрасывает эту петлю за борт и включает в ней ток. Закон Ленца утверждает, что поток поля будет пытаться остаться постоянным. Это заставит площадь токовой петли увеличиваться пока она не примет форму окружность без всякой посторонней помощи. Все что теперь требуется - подвесить к петле космический корабль на нескольких стропах (вантах) соединенных вместе (Рис. 1).
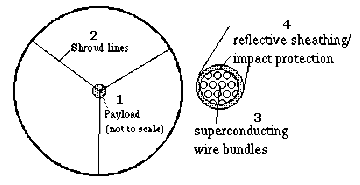
Рис. 1. На схеме на английском:
1 Полезная нагрузка (показана не в масштабе). 2 Стропы (ванты). 3 Жгут сверхпроводниковых кабелей. 4 Зеркальная обшивка и метеоритная защита.
Если мы имеем направленный поток заряженных частиц, то можно рассматривать два крайних случая ориентации магнитного паруса (угла атаки) к нему. Самый простой случай - симметричный или осевой (symmetric или axial) . Он так называется, потому что частицы движутся параллельно оси магнитного поля и рассеиваются (отражаются им) симметрично. Частицы, вступающие в такое взаимодействие летят не строго по оси поля, а чуть под углом и значит испытывают боковое ускорение. В результате передают часть своего z-импульса полю и следовательно кораблю.
Другое положение паруса - ассиметричная или нормальная (asymmetric or normal) ориентация является несколько менее очевидной. Если дипольный момент ориентирован по оси Z (то есть сама петля лежит в плоскости XY) и, предположим, частицы влетают со скоростью V=Vx, то они будут отклоняться полем петли по оси Y, получая по этой оси ускорение. Таким образом, импульс частиц по оси Х передается парусу вдоль оси Y.
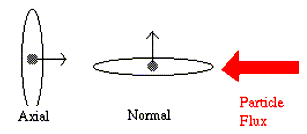
Рис. 2
Представим теперь корабль на круговой орбите вокруг Солнца. В первом случае мы имеем эквивалент тяги, направленной наружу во втором - вариант тяги направленной по касательной к нашей орбите, очень полезный вариант, между прочим! Направлением и силой тяги можно управлять, изменяя силу тока в петле и ее ориентацию в пространстве. В действительности с таким парусом можно осуществлять очень сложные маневры, как утверждает Зубрин и Эндрю (Zubrin and Andrews,91).
2 Моделирование магнитного паруса
Параметры проекта
Так как магнитный парус никогда не строился, да никто пока и не собирается его строит, мы должны определить предварительные параметры нашего паруса на пустом месте. В настоящий момент никакое исследование не опирается на идею двойной петли или более сложной конфигурации и нет никакой причины полагать, что какая-нибудь подобная структура была бы лучше одинарной токовой петли. Поэтому и мы не будем мудрствовать.
Ясно, что мы намерены максимизировать охватываемую парусом площадь, при минимуме используемой для этого массы. Эффективность нашего паруса зависить от напряженности магнитного поля, которое он сможет сгенерировать. При радиусе R эффективная площадь захвата пропорциональна R2 в то время как напряженность магнитного поля пропорциональна R-2. Масса паруса пропорциональна R. Таким образом, давайте выберем некое среднее значение для размеров паруса, скажем 10 км. (Обратите внимание, если вы не знакомы с данной областью проектирования: 10 км - крошечная величина по сравнению с реально возможными габаритами солнечных парусов)
Напряженность поля так же пропорциональна I (силе тока), поэтому мы должны стараться получить максимальную силу тока в нашем кабеле. Дабы свести к нулю неизбежные при сильных токах потери на омическое сопротивление хорошая идея использовать для материала петли сверхпроводник. Хотя эта идея избавляет нас от необходимости иметь на борту корабля мощный источник тока (солнечные батареи, изотопно-термические генераторы, аккумуляторы и т.д.), но она привносит с собой и типичные проблемы, связанную с критической температуры работы сверхпроводника, а также с ограничением на максимальный ток, при котором сверхпроводимость разрушается.
Недавно открытые высокотемпературные сверхпроводники облегчают решение этой проблемы. Ba2Cu3O7Y, новый керамический сверхпроводник, имеет критический ток 1010 А/м2 (Zubrin & Andrews, 91) и критическую температуру 90 K (CRC). Хотя фоновая температура в космосе ~3 К, что не предвещает никакой угрозы, но прямые солнечные лучи могут быстро поднять температуру выше критической. Однако с тонким слоем зеркальной изоляции (которая дополнительно будет служить защитой от микрометеоритов) необходимый температурный режим для сверхпроводников вполне может поддерживаться и в прямых солнечных лучах. Массу строп, не мудрствуя лукаво, мы брать в расчет не будем, так как наша модель - приблизительная модель и не более.
Плотность выбранного сверхпроводника примем порядка 5 грамм/см3. Если мы примем для него диаметр 12 мм (как у хорошей альпинисткой веревки), то наш провод мог бы проводить мега-Амперы тока и все еще поддерживать сверхпроводимость. Изоляция может быть довольно легкой (0.5 г/см3) и довольно тонкой (~3 мм). Это приведет к тому, что выбранная нами токовая петля будет иметь массу 36 000 кг или 36 тонн.
Таблица 1. Параметры проекта
| Параметр |
Значение |
| Радиус паруса |
10 км |
| радиус кабеля |
6 мм |
| материал |
Ba2Cu3O7Y |
| максимальный ток |
106 А |
| критическая температура |
90 К |
| поле в центре |
6.28x10-5 Т |
| масса паруса |
36 000 кг |
Моделирование, поведение
Чтобы получить некоторое представление о поведении магнитного паруса, был написан программный код (см. Приложение) который моделирует траектории частиц в магнитном поле. Рассматриваемые в модели частицы - это компоненты солнечного ветра, который состоит в основном из протонов и электронов. Мы выбрали только протоны, потому что они несут примерно в 1000 раз больший импульс, чем электроны и таким образом именно они и важны для получения тяги космическим кораблем. Характерной скоростью было выбрано значение в 500 км/с - приближение к средней скорости для этих частиц на расстоянии 1 а. е. от Солнца. Реально скорость на этом расстоянии изменяется от 300 до 700 км/с в зависимости от солнечной активности и расположения солнечных пятен (Zelik and Smith).
Выбирая некоторую геометрическую базу (рис. 3) вектор из начала координат (который для удобства помещен в центр петли) направленный к петле вектор r' был выражен через экваториальный угол пи.
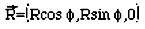
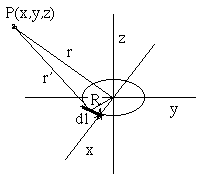
Рис. 3
Бесконечно малый вектор тока в петле Idl был найден как R x eZ так как петля, как известно, находится в XY-плоскости, он будет перпендикулярным к радиусу:
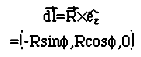
Вектор r' от текущего элемента витка до частицы P определяется через радиус-вектор r этой частицы из начала координат:

В отличии от приблизительной модели с диполем, которые использовали Эндрю и Зубрин (Andrews and Zubrin q.v.) я использовал полное уравнение Био-Савара для каждой ординаты. Это представляется более точным подходом, поскольку радиус (видимо так называемого ларморовского круга прим. перев.) протонов часто близок к радиусу выбранной петли и тогда приближение в виде диполя становится чересчур грубым.
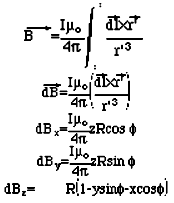
При численном интегрировании по петле, для выбранной точки расположения протона находятся проекции вектора B на оси. Тогда проекции ускорений частицы на оси следуют из соответствующих проекций напряженности поля по закону для силы Лоренца.
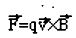
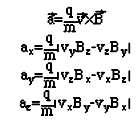
На основании этого на каждом шаге вычисляется новая скорость и позиция частицы, после чего процесс повторяется снова (итерируется). Полученные таким образом данные обработаны пакетом Mathematica, где на основе них интерполированы и построены параметрические кривые. Мы моделировали траектории частиц для двух ориентаций петли с током 50 КA и 1 МА, что показаны на рис 4. Все изображения охватывают промежуток времени в 250 миллисекунд.

Рисунок 4a. Осевая конфигурация для тока намного меньшего, чем Imах. Частицы летят снизу (-Z) со скоростью 500 км/с. Размер токовой петли не в масштабе и увеличен для наглядности. Только те частицы, что проходят очень близко к петле испытывают большие отклонения траектории.
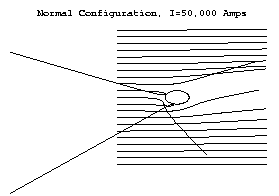
Рисунок 4b. Нормальная конфигурация при низком токе. Частицы движутся слева в плоскости XY. Нет никакого отклонения в плоскости Z. Вообще говоря, поток практически не перехватывается.
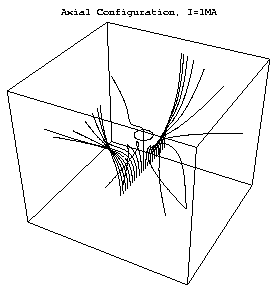
Рисунок 4с. Осевая конфигурация для I ~Imax. Обратите внимание на симметрию рассеивания.

Рисунок 4d. Нормальная конфигурация для почти критического тока. Частицы и близко не приближаются к токовому кольцу. И снова нет никакого рассеивания вне плоскости. Обратите внимание на турбулентный след позади паруса.
Моделирование, результаты
После того как программа моделирования поведения частиц была усовершенствована, ее использовали для оценки эффективности двигателя методом Монте-Карло. Большое количество частиц со случайными начальными координатами было введено в систему и выполнено моделирование поведения каждой. Были испытаны четыре различных ситуации (представленные на рис 4 a-d). Для каждой частицы было найдено изменение ее скорости. На большом количестве частиц было найдено среднее изменение скорости в прилегающей области, что позволило нам найти сечение рассеивания:
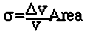
Таблица 2. Сечение рассеивания. Результаты моделирования методом Монте-Карло.
| конфигур. |
I А |
dV/част. |
частиц |
Хсечения(м2) |
фракция Xсеч. |
| Осевая |
50К |
0.031 |
250 |
2.8E5 |
0.001 |
| Осевая |
1M |
2.48E4 |
200 |
4.97E8 |
1.58 |
| Нормальная |
50К |
1.63E4 |
200 |
3.2E8 |
0.76 |
| Нормальная |
1M |
4.7E5 |
200 |
3.9E10 |
30 |
И так, величина силы тока сильно влияет на сечении рассеивания магнитного паруса. Это, однако, очень грубая оценка (из-за ограничений машинного времени, вычисления для большего числа частиц не было проведено). При 5-и секундном расходе машинного времени на частицу большая точность потребует длительного времени расчета!
Чтобы сделать вывод из нашего моделирование, давайте определимся относительно способностей этого судна. Выше мы вычислили массу судна в 36 тонн. В окрестностях Земли плотность частиц оценивается между 0.4 и 80 миллионом частиц на м3 (опять же зависит от погоды на Солнце (Zelik and Smith)). Если выбрать промежуточное значение 2x107 протонов/м3 и оценить среднюю скорость частиц в 500 км/с, мы можем видеть, что поток (плотность) импульса:
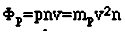
Тогда сила, оказывающая давление на весь магнитный парус:
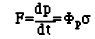 =4.15 Ньютон. =4.15 Ньютон.
для осевой конфигурации и при максимальном токе. Это сопоставимо с результатом, который вычислили Эндрю и Зубрин (Zubrin and Andrews) в 19.8 Ньютон. При делении на массу паруса мы получим ускорение 0.0001 м/с2 . Ориентировав парус нормально к потоку, мы увеличили бы ускорение до 0.009 м/с2. Этот результат так же вполне согласуются с вычислениями для подобной ситуации сделанными независимо от нас Эндрю и Зубриным (Zubrin and Andrews, 91). Расхождение вызваны различиями в физических моделях полей и материалами конструкции.
3 Заключение
Ясно, что большое преимущество магнитного паруса - его способность работать на "окружающим" его источником энергии и отсутствие какого-либо тяжелого топлива на борту. Технология относительно проста и по существу возможна уже сегодня. Кроме того, это такая технология, которая может быть приспособлена для существующих уже корабли или тех, что в ближайшем будущем появятся. Приспособлена, с небольшими затратами.
Одной из самых больших опасностей для людей в космосе, особенно в случае длительных рейса вдали от защиты земной магнитосферы являются проникающее излучение и высокоэнергетические космические частицы. В связи с этим очень кстати что магнитосфера паруса отклоняет любые высокоэнергетические заряженные частицы от центра проводящей петли. Хотя это не сильно помогает от нейтральных частиц и гамма-лучей, для чего должны использоваться обычные экраны (типа резервуаров с водой).
На первый взгляд может показаться, что сам космический корабль нужно будет защищать от собственных сильных магнитных полей. Однако из-за огромного радиуса токового контура напряженность поля в центре 10-и км паруса будет только 6х10-11 Тесла на ампер тока в петле. Для принятого нами рабочего тока в мегаампер напряженность поля в центре будет все еще 63 мкТ (микро Тесла 10-6) или 0.63 Гаусс. Это сопоставимо с напряженностью магнитного поля Земли. А такое поле не представляет никакой опасности ни для людей, ни для машин.
Еще одно преимущество. В то время как разворачивание двумерных структур (типа световых парусов) представляет собой сложную проблему, требующую специальных методов сворачивания, одномерная структура (типа петли магнитного паруса) может быть намотана на специальную катушку и легко размотана в нужный момент. Кроме того, в полете всегда возникает необходимость изменять размер паруса (в терминологии парусного спорта "рифлить") для регулирования параметров тяги, что обеспечивает определенную степень навигационной свободы. Магнитный парус в этом смысле проще светового.
Но существуют два недостатка, присущие идее плаванья под магнитным парусом. Первый, который присущ и солнечным парусом, в том, что плотность импульса разгоняющей среды уменьшается с r -2. Однако в случае магнитного паруса имеется положительная сторона всего этого. Солнечный ветер имеет тенденцию к ускорению по мере удаления от Солнца, поэтому, хотя плотность частиц падает, импульс каждой повышается.
Другой и куда более серьезный недостаток, имеющийся исключительно у магнитного паруса - непредсказуемость "тяговой системы". Обычно, синхронизация сроков проведения космических маневров очень важно, когда имеешь дело с траекториями кораблей. Орбиты скрупулезно рассчитаны на несколько лет вперед. Но тяга магнитного паруса, а следовательно и все сроки мисси, сильно зависит от плотности и скорости прилетающих от Солнца протонов. Как было уже указано в этой работе, скорость солнечного ветра и его плотность очень сильно меняются в зависимости от условий на поверхности светила. К счастью, имеется способ сделать навигационную обстановку значительно более предсказуемой. Так как парус может менять силу, направление тяги и фактически зависать в потоке (парить над Солнцем), судно может двигаться по стандартной орбите и в случае опережения ожидать в точке встречи, пока цель не прибудет туда сама. Соответствующая для этого скорость - вопрос настройки паруса под поток и выбор угла атаки. Детали этого вычисления за пределами данной работы, но об этом кратко есть у (Zubrin and Andrews 91).
Очень сомнительно, чтобы магнитный парус служил средством разгона для скоростного межзвездного путешествия (здесь автор неправ, к 1997-му существовал ряд проектов и оценок межзвездных систем, разгоняемых потоком заряженных частиц или материи. Все они используют именно механизм магнитного паруса. Еще одно упущение. "Нормальная" тяга может использоваться для корректировки курса звездолета. Прим. перев.). Но магнитный парус мог бы оказаться "крайне приятным" дополнением как средство торможения межзвездного судна у цели. В этом случае речь идет не о магнитном поле, на которое обрушивается поток заряженных частиц, а скорее о магнитное поле, несущемся через пространство, наполненное неподвижными заряженными частицами. Межзвездное пространство заполнено частицами небольшая часть из которых заряжена, а остальные - нет. Однако удар, произведенный врезающейся на большой скорости магнитосферой магнитного паруса (так называемый в гидро- и магнитодинамике Bow Shock, "ударный шок") мог бы послужить очень эффективным средством ионизации среды перед парусом-парашютом. Корме того, так как относительная скорость набегающей среды будет значительно выше, чем у солнечного ветра, эффективность магнитного паруса как тормоза (магнитного парашюта) тоже повышается. Поэтому мы можем легко представить себе межзвездный корабль, который разворачивает магнитные крылья, чтобы затормозить свой бешенный бег и исследовать далекую звезду...
4 References
(CRC) CRC Handbood of Chemistry and Physics, David R. Lide (Ed.) 72nd Edition (student edition) 1991-92, pp12-156.
(Zubrin and Andrews 90) Andrews, D. G., and Zubrin, R. M., "Magnetic Sails and Interstellar Travel," Journal of the British Interplanetary Society, Vol43, pp265-272, 1990.
(Zubrin and Andrews 91) Andrews, D. G., and Zubrin, R. M., "Magnetic Sails and Interplanetary Travel," Journal of the British Interplanetary Society, Vol. 28, No. 2, March-April 1991, pp197-203.
(Zelik and Smith) Introductory Astronomy and Astrophysics Saunders College Publishing, Philadelphia, PA, 1987, pp.189-199.
Purcell, E. M., Electricity and Magnetism, Berkeley Physics Course Vol. 2, McGraw Hill, NY, 1985, pp.400-409.
Griffiths, D. J., Introduction to Electrodynamics, Prentic-Hall, Englewood Cliffs, NJ, 1981, pp.184-188.
5 Техническое приложение
Ниже представлена основная часть кода на Фортране применявшегося для моделирования. Программа отслеживает движение одной частицы с заданной начальной скоростью и координатами через магнитное поле, вычисляет его и находит полную дельта-V частицы. Файл данных заполняется для каждого интервала времени текущей координатой (x, y, z) и скоростью протона на каждом шаге. Этот код может быть легко изменен для расчета поведения множества частиц или моделирования методом Монте-Карло. Для понимания кода нужно обладать азами языка программирования Fortran77.
program magtracer
c by Charles Danforth for JHU 171-304
c 4-24-97 last modified 4-29-97
c Variable declarations
real b(3) (magnetic field
real p,dp (integration angle, interval
integer t,tmax,dt (time, max, interval
real rr2,g,current,const (radius squared, loop rad
real r(3,10000) (particle coordinate(time)
real v(3,10000) (particle velocity(time)
real a(3,10000) (particle accelleration(time)
real radius (scalar dist from origin
real dv(3),deltav (deltaV vector and scalar
real Pi,mu0,q,m (physical constants (SI units)
c Constant Definitions
Pi=3.1415926535
mu0=4*Pi*.0000001
q=1.6E-19
m=1.672E-27
c Open data file
open(1,file='magtracer.output')
c &&& multiparticle loop start &&&
c ---- INITIAL CONDITIONS ----
c positions in meters (1,2,3)---(x,y,z)
r(1,1)=-50000
r(2,1)=(yinit)*10000
r(3,1)=0
c velocities in meters/second
v(1,1)=500000
v(2,1)=0
v(3,1)=0
c ---- PARAMETERS ----
c Set number of time steps TMAX in units of dt
tmax=250
dt=.001
c Set dp increment (radians)
dp=.01
c Set mag field scale factors current=I(amps), loop radius=g(meters)
current=1E6
g=10000
const=I*mu0*dp/(8*Pi**2)
c write initial condition in the data file
write(1,*),1,r(1,1),r(2,1),r(3,1),v(1,1),v(2,1),v(3,1)
c ### Start moving the particle ##############
do t=2,tmax
radius=(r(1,t-1)**2+r(2,t-1)**2+r(3,t-1)**2)**.5
c ^^^^^^ FIND MAGNETIC FIELD at current particle location ^^^^^^^
c Code offers three options for magnetic field. The first is the
c full Biot-Savart law which should be universally applicable.
c Second is the magnetic dipole approximation which is very similar
c to the first but takes much less time to run since it involves no
c numerical integration routines.
c Thirdly, for comparison, a uniform field is presented.
c &&&&& BIOT-SAVART LAW FOR CURRENT LOOP (radius 1) &&&&&
do i=1,3
b(i)=0
end do
c Numerically Integrate around loop, dl X r / r^3
do p=0,6.28,dp
rr2=((r(1,t-1)-g*cos(p))**2+(r(2,t-1)-g*sin(p))**2+r(3,t-1)**2)
b(1)=b(1)+const*r(3,t-1)*g*cos(p)/rr2**1.5
b(2)=b(2)+const*g*sin(p)*r(3,t-1)/rr2**1.5
b(3)=b(3)-const*g*(r(2,t-1)*sin(p)-r(1,t-1)*cos(p)+1)/rr2**1.5
end do
c &&&&& DIPOLE FIELD (dipole approx) &&&&&
c >> Current Loop in xy plane, dipole in z direction <<
c if(radius.lt.0.00001) then
c b(1)=0
c b(2)=0
c b(3)=bo
c else
c b(1)=bo*3*r(1,t-1)*r(3,t-1)/(radius)**5
c b(2)=bo*3*r(2,t-1)*r(3,t-1)/(radius)**5
c b(3)=bo*(2*r(3,t-1)**2-r(1,t-1)**2-r(2,t-1)**2)/(radius)**5
c end if
c
c &&&&& CONSTANT FIELD &&&&&
c >> Constant field in z direction <<
c b(1)=0
c b(2)=0
c b(3)=bo
c Find the accelleration for this step (componentwise Lorenz Force Law)
a(1,t)=q/m*(v(2,t-1)*b(3)-v(3,t-1)*b(2))
a(2,t)=q/m*(v(3,t-1)*b(1)-v(1,t-1)*b(3))
a(3,t)=q/m*(v(1,t-1)*b(2)-v(2,t-1)*b(1))
c Move the particle in r and v
do i=1,3
v(i,t)=v(i,t-1)+a(i,t)*dt
r(i,t)=r(i,t-1)+v(i,t)*dt
end do
c Print everything to a file and screen
write(1,*),t,r(1,t),r(2,t),r(3,t),v(1,t),v(2,t),v(3,t)
print*,t,r(1,t),r(2,t),r(3,t),v(1,t),v(2,t),v(3,t),radius
end do
c Calculate delta-v of particle (and hence of the field)
do i=1,3
dv(i)=v(i,tmax)-v(i,1)
end do
deltav=(dv(1)**2+dv(2)**2+dv(3)**2)**.5
print*,'DELTA V=',dv(1),dv(2),dv(3),deltav
c &&& End of multiparticle loop &&&
close(1)
end |
Перевод А. Семенов, май 2008 г.
первоисточник
__________________________________________________
[ вверх ] [ оглавление ]

Оптимизирован под Internet Explorer 1024X768
средний размер шрифта
Дизайн A Semenov
|