Г РИЗОНТ РИЗОНТ
в_о_з_м_о_ж_н_о_г_о______________________________________
[ оглавление ]

|
ЗВЕЗДОЛЕТЫ НА СОЛНЕЧНЫХ ПАРУCАХ:
КЛИПЕРА ГАЛАКТИКИ
Журнал Британского межпланетного общества
выпуск 34 стр. 371-380
1981 г.
SOLAR SAIL STARSHIPS: THE CLIPPER SHIPS OF THE GALAXY
Journal of the British Interplanetary Society,
Vol. 34, pp. 371-380, 1981. JBIS
|
 Грегори Л.
Грегори Л.
Мэтлофф
GREGORY L. MATLOFF *
Department of Applied Science, New York University, 26-36 Stuyvesant Street, New York, New York 10003, USA.
|
 Юджин
Юджин
Малов
EUGENE MALLOVE
Astronomy New England, 215 Highland Street, Holliston, Mass. 07146, USA.
|
* Currently on leave of absence with the Systems and Applied Sciences Corporation, Riverdale, Md. 10840, USA.
Мы рассмотрим конструкцию солнечного паруса 10-8 - 10-7 метров (м) толщиной, изготовленного в космосе и предназначенного для межзвездной миссии. Предполагается, что солнечный парус будет частично или полностью развернут позади намного более массивного обломка астероида, который послужит ему щитом и источником тени. Парус, выйдет из тени и наполнится солнечным светом на расстоянии 1,5x109 м от светила, проходя в перигелии по почти гиперболической или параболической траектории. Оборудование зонда-автомата может быть нанесена как тонкая структура, распределенная на теневой стороне такого паруса. Большой обитаемый модуль с командой из людей на борту, может быть подвешен на алмазных или медных тросах-стропах позади паруса. Проблемы с нагрузками в тросах и парусе, использование гравитационного маневра у планет-гигантов, способ развертывания паруса, термический режим и предварительный проект мисси - все рассматривается. Технологии ближайшего времени могут быть использованы для запуска компактного зонда-робота, который достигнет Альфы Центавры в пределах приблизительно 350-и лет. Продемонстрировано, что намного больший пилотируемый корабль-колония, разгон которого ограничен максимально приемлемым для людей ускорением, мог бы, используя солнечный парус, достигнуть Альфы Центавры в течение 900 - 1400 лет. И в конце концов, указано, что когда в будущем, наше Солнце через 4x109 лет превратиться в красного гиганта, возможность для использования солнечного паруса как межзвездного ускорителя значительно возрастет.
1. ВВЕДЕНИЕ
ХОТЯ ТЕОРЕТИЧЕСКИЙ АНАЛИЗ солнечного паруса на протяжении последнего десятилетия уже выполнялся [1], но требовался некоторый прогресса в технологии материалов, прежде чем этот принцип мог бы рассматриваться в приложении к реальным межпланетным миссиям. Недавно были сделаны оценки ряда таких проектов, в качестве привода для зонда который планируют послать на встречу с кометой Галлея в 1986-м году [2], а теперь предпринимается анализ более дерзких идей в приложении этой концепции для индустриализации и колонизации космоса [3].
Идея использовать солнечный парус для экспедиций в межзвездное пространство еще не была подвергнута детальному анализу, хотя паруса вообще уже были предложены как движители межзвездной миссии, разгоняемой лазерным лучом [4,5]. Форвард выдвинул идею, что тонкопленочный робот-зонд мог бы быть нанесен на теневую сторону тончайшего паруса, который, используя гравитационный маневр, прошел бы у самого Солнца и там раскрыл свой парус для разгона к звездам [6]. Вивинг (Viewing) выдвинул предположение, что идея солнечного паруса позволяет строить другим цивилизациям "безвредные звездолеты" и такой привод из чисто экономических соображений, мог бы быть более распространены в Галактике, чем намного более быстрые суда, использующие термоядерный синтез или антиматерию [7].
Межзвездная пилотируемая миссия, использующая солнечный парус, будет долгой. Большая космическая колония, подвешенная на алмазных стропах к полотнищу парусу, будет ограничена в скорости полета из-за максимально допустимого ускорения, что в свою очередь ограничивается способностью людей переносить перегрузки, а также пределом прочности парусов и строп. Поэтому на такое межзвездное путешествие потребуется приблизительно 1000 лет.
Подобные длинные перелеты не стоит сразу отвергать как неблагоразумную затею, так как по крайней мере минимизированный автоматический исследовательский зонд, с очень большой длительностью жизни оборудования, в конечном итоге выглядит вполне возможным [6], а автономные космические поселения, наподобие предложенных О'Нейлом, могут оказаться социально достаточно комфортны и устойчивы для того чтобы выдержать длительное межзвездное путешествие [8]. Кроме того, если мы разовьемся в цивилизацию, владеющую Солнечной системой, которая здесь просуществует приблизительно четыре миллиарда лет, в будущем условия для разгона кораблей солнечным парусом значительно облегчатся, что приведет к решительному сокращению сроков межзвездных путешествий [9]. В этом смысле, как мы покажем ниже, солнечный парус может стать "спасательной технологией", которая позволит цивилизации II-го типа [10] избежать страшных последствий связанных с расширением нашей родной звезды.
В следующих разделах мы будем рассматривать кинематику паруса, нагрузку, стратегию раскрытия его полотнища, разные аспекты дизайна миссии, сам межзвездный полет и торможение у цели. Для начала мы рассмотрим кинематику полностью и частично развернутого паруса.
ВРЕЗКА 1 от "Горизонта возможного"
Грегори Мэтлофф:
"За некоторым исключением мои статьи сосредоточены на межзвездном полете, использующем известную физику. Хотя они требуют столетия и тысячелетия времени для завершения путешествия, мы можем, по крайней мере, оценить эти методы, опираясь на современные знания."
|

|
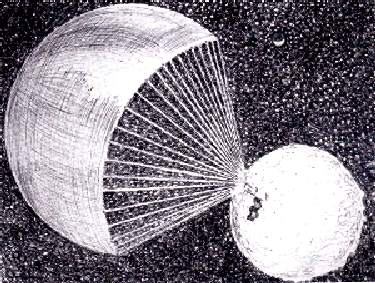
Рис 4. На расстоянии нескольких радиусов Солнца от его центра, частично свернутый межзвездный солнечный парус, выходит из тени своего массивного прикрытия. Ускоряясь из перигелия, парус разворачивается, постепенно сбрасывая балласт. Назначение балласта - смягчить динамику ускорения.
|
|
Рис. 5. Когда парус пересекает орбиты внутренних планет процесс раскрытия паруса уже завершен. Ускорение по мере удаления от Солнца начинает падать по закону обратных квадратов.
|
|

|
Рис. 6. Далеко от Солнца давление света фактически падает до нуля. Роботы и нанороботы (наподобие "смотрителей" предложенных BIS для проекта "Дедал") сворачивают парус и кабеля вокруг полезной нагрузки, чтобы обеспечить дополнительную защиту от космического излучения. Много столетий спустя парус развернется снова чтобы затормозить корабль у зведы-цели.
|
|
Эта серия иллюстраций взята на сайте Г. Мэтлоффа gregmatloff.com.Источник не ясен. Но это явно страница из книги. Возможно THE STAR FLIGHT HANDBOOK? Автор рисунков так же не известен. Возможно сам Мэтлоф?
|
2. КИНЕМАТИКА СОЛНЕЧНОГО ПАРУСА
Рисунок 1 представляет солнечный парус с полезной нагрузкой в варианте тонкопленочного автоматического зонда и в варианте автономного мобильного поселения людей.
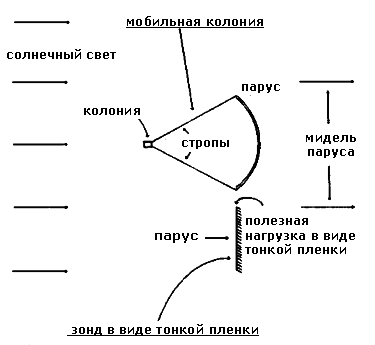
Рис.1 Положение парусов, строп и полезной нагрузки
На рисунке 2 мы показываем возможный метод разворачивания паруса возле Солнца.
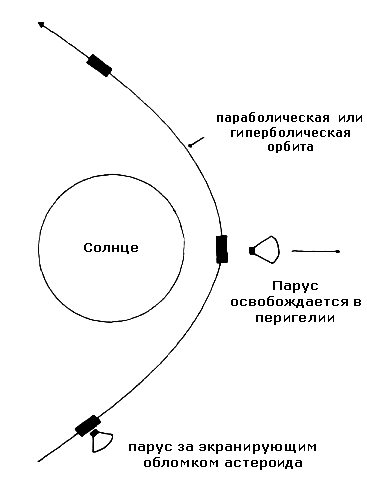
Рис.2 Использование астероидного обломка или специального экрана для разворачивания паруса у поверхности Солнца
Парус либо частично, либо полностью раскрытый выводится на параболическую или гиперболическую орбиту с перигелием приблизительно 0,01-0,03 а.е. (астрономические единицы) от центра Солнца. Согласно Эйрике (Ehricke) минимально-возможное расстояние на которое можно приблизиться к Солнцу (в перигелии) - 0,01 а.е [11]. Для параболической орбиты в перигелии скорость будет V0 <= корень(2)VCIRC ("<=" - читать "меньше или равно") , где VCIRC - скорость круговой орбиты на расстоянии выбранного нами перигелия. Для r0 = 0,01 а.е., V0 <= 0,0014с (c - скорость света), для r0 = 0,03 а.е., V0 <= 0,0008с. Если на скорости 18-24 км/с выполнить гравитационный маневр возле Сатурна, то гиперболическая скорость в r0 = 0,01 а.е. будет V0 <= 0,002с, относительно Солнца [11].
Для тонкопленочного зонда (Mprobe) и обитаемой колонии запускаемой парусом (Mhabital), показанных на рисунке 1, общая масса в момент выхода из тени может быть выражена так, (если парус имеет круглую форму):
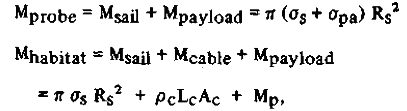 (1) (1)
Где bs ("b" - "сигма") поверхностная плотность паруса (кг/м2), bpa поверхностная плотность тонко-пленочной полезной нагрузки - оборудование зонда (кг/м2), Rs (м) - радиус проекции паруса на Солцне (мидель радиуса паруса к Солнцу) pc (кг/м3) - плотность материала из которого изготовлены троса строп ("p" - читать "ро"), Lc (м) - длина строп (как показано ниже, Lc > Rs), Ac (м2) - суммарная площадь сечения всех строповых тросов и Mp масса полезной нагрузки.
Если для солнечного паруса нормально ориентированного к поверхности светила использовать закон обратных квадратов убывания энергии солнечного потока в зависимости от дистанции r (от центра Солнца), то получим:
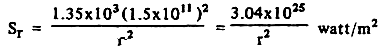 (2) (2)
(Все количественные параметры, используемые в этой работе, представлены в системе СИ, если обратное не оговорено специально).
Согласно Тсу (Tsu) [1] для паруса со 100%-ой отражающей способностью давление света можно записать как 2Sr/с, где с - скорость света. Для паруса, с коэффициентом отражения k, давление солнечного потока можно записать [(1+ k)/2] Sr/с. Таким образом, парус с 95%-ым коэффициентом отражения снижает давление солнечной радиации на 2,5%. Поэтому радиальное ускорение космического судна под действием давления солнечного света можно записать:
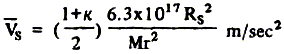 (3) (3)
Согласно элементарному закону сохранения энергии, скорость солнечного паруса V на дистанции r от центра Солнца можно выразить:
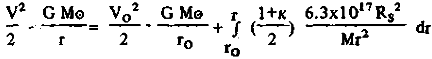 (4) (4)
где G - гравитационная постоянная, M0 - масса Солнца, а индекс "0" всюду означает начальные условия. Все это опирается на два предположения, сделанные в (4), о том, что ось паруса всегда будет направлена к Солнцу, и парус полностью развернут на всем промежутке от r0 до r. Дополнительная гиперболическая скорость паруса уже позволяет ему вырваться из гравитационного поля Солнца, тогда Vinf ("inf" - читать "бесконечность") полученная из (4), может рассматриваться как изменение скорости паруса с r0 до бесконечности:
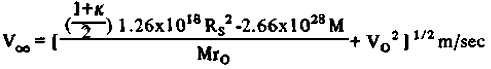 (5) (5)
Мы можем проанализировать работу больших солнечных парусов, исходя из их эффективной поверхностной плотности, be, для паруса+пленочная_полезная_нагрузка или парус+стропы+полезная_нагрузка. Согласно уравнению (5):
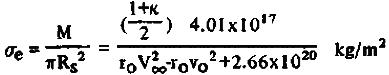 (6) (6)
Используя уравнение (3), максимальное ускорение корабля должно быть связано с be:
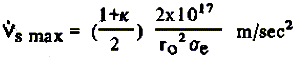 (7) (7)
Дрекслер (Drexler) отмечал, что в конечном итоге можно будет добиться толщины 10-7 м для паруса созданного в космосе и что имеется некоторая теоретическая возможность изготовить паруса толщиной 10-8 м. Тсу, проектирует материал для паруса, которые должны выдерживать 1,18g [1]. Таблица 1 представляет решение уравнений (6) и (7) для различных конечных скоростей и скоростей в перигелии. Для простоты расчетов здесь отражательная способность паруса была принята 100%.
ТАБЛИЦА 1. Результат разгона солнечного паруса полностью разверзнутого в перигелии: Vinf - скорость на бесконечности, V0- скорость в перигелии, с - скорость света, be- поверхностная плотность, масса всей миссии деленная на площадь паруса, V*s_max - максимальное ускорение.
| Vinf/c |
V0/с |
be (кг/м2) |
V*s_max (gearth) |
| 0,0014 |
0,0014 |
1,51x10-3 |
6,02 |
0,002 |
- " - |
7,40x10-4 |
12,75 |
0,003 |
- " - |
3,30 x10-4 |
27,51 |
0,004 |
- " - |
1,86x10-4 |
48,89 |
0,005 |
- " - |
1,19x10-4 |
76,37 |
0,007 |
- " - |
6,06x10-5 |
149,65 |
0,009 |
- " - |
3,67x10-5 |
247,37 |
0,011 |
- " - |
2,45x10-5 |
369,51 |
0,012 |
- " - |
2,06x10-5 |
439,00 |
0,013 |
- " - |
1,76x10-5 |
516,09 |
0,015 |
- " - |
1,32x10-5 |
687,09 |
0,002 |
0,002 |
4,29x10-3 |
6,02 |
0,003 |
- " - |
4,26 x10-4 |
21,28 |
0,004 |
- " - |
2,13x10-4 |
42,62 |
0,005 |
- " - |
1,29x10-4 |
70,14 |
0,007 |
- " - |
6,32x10-5 |
143,42 |
0,009 |
- " - |
3,76x10-5 |
241,14 |
0,011 |
- " - |
2,50x10-5 |
363,29 |
0,013 |
- " - |
1,78x10-5 |
509,86 |
0,015 |
- " - |
0,33x10-5 |
680,86 |
Оценивая таблицу 1, стоит отметить, что на расстоянии 0,01 а.е. от Солнца, гравитационное ускорение к Солнцу составляет 6,61 gearth , где gearth - ускорение свободного падения у поверхности Земли. Хотя люди выдерживали и 45 gearth но в течении долей секунды, рекордное длительное ускорения без болезненных последствий и потери сознания 17 gearth в течение четырех минут [12,13]. Таким образом, даже с гравитационным маневром у Сатурна на скорости 18-74 км/с и получении в результате этого в перигелии V0 = 0,002с, полностью развернутый парус для разгона колонии с людьми окажется ограниченным Vinf <= 0,003c, что получено интерполяцией предельного ускорения в 17 gearth.
Чтобы и дальше рассматривать кинематику запускаемой солнечным парусом межзвездной пилотируемой колонии, мы должны добиться ограничения эффективного радиус солнечного паруса так, чтобы астронавты никак не могли испытать при разгоне ускорение, большее, чем предельно допустимое. Этого можно добиться, разворачивая парус постепенно, сохраняя отношение Rs/r =constanta , пока корабль находится недалеко от Солнца. Далее, после того как парус развернется полностью, разгон происходит уже с Rs = constanta. Ускорение, полученное опытным путем для корабля с экипажем, подставленное в уравнение (3) и суммарное ускорение корабля относительно Солнца может быть рассчитано, вычитая гравитационное ускорение к Солнцу из уравнения (4).
Требование максимального допустимого ускорения V*A (с точкой, dt) и использование Rs/r = constanta с уравнением (3) приводит к отношению,
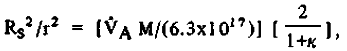 (8) (8)
для первоначального этапа ускорения. Далее мы определим VP - скорость в перигелии (начала разворачивания парусов), rP - дистанция в перигелии. Еще раз, V0 - скорость в момент, когда парус уже полностью развернут и r0 - дистанция от паруса до центра Солнца, когда тот полностью развернут. Теперь, с этого момента ускорение V*[с точкой, dt] = V dv/dr,
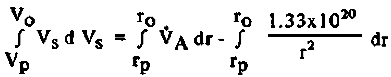 (9) (9)
здесь замена GMО = 1,33x1020. Интегрируя, мы может связать начальные (в перигелии) условия с условиями старта в точке "полностью развернутого паруса" следующим образом:
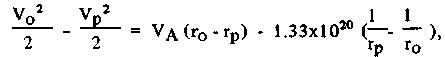 (10) (10)
что ведет к:
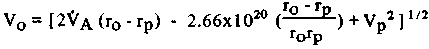 (11) (11)
и, через уравнение (3) получаем:
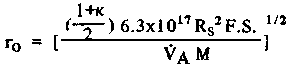 (12) (12)
где Rs(F.S.)- радиус полностью развернутого паруса.
Уравнения (11) и (12) надо подставить в уравнение (5), в отношение Vinf для начальных условий в перигелии. Решение этих уравнений, рассчитанное для 100% -но отражающего паруса, представлено на рисунке 3 в предположении нескольких скоростей в перигелии и значения be = M/( п Rs2 ). Обратите внимание на различие конфигураций позволяющих путешествовать к Альфа Центавра за 800-1300 лет, с пределом ускорения от 10 до 20 gearth.
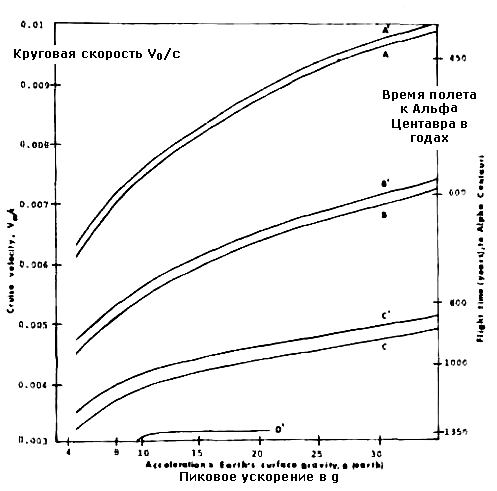
Рисунок 3. Поведение солнечного паруса-звездолета с частично развернутым парусом в перигелии, который продолжает разворачиваться так, что Rs/r = constanta до полного раскрытия паруса. Rs - радиус эффективной проекции паруса к Солнцу (радиус миделя) и r - дистанция до центра Солнца. Случаи А, В, С, D соответствуют отношению массы мисси к площади паруса (поверхностная плотность), соответственно: 1,18x10-5; 3,73x10-5; 1,18x10-4 и 3,73x10-4 кг/м2. Штрих отличает случай, когда скорость в перигелии равна 0,002c, от случая (без штриха), когда скорость в перигелии равна 0,0014с.
Это неплохой результат для солнечных межзвездных парусов, так как эффективная поверхностная плотность здесь в 3-10 раз больше установленного Дрекслером минимума и позволяет выполнить задачу даже без маневра у Сатурна. Потому что, как мы увидим в следующем разделе, соображения связанные с динамикой напряжений в парусе добавят к проектируемой системе дополнительную массу.
ВРЕЗКА 2 от "Горизонта возможного"
THE STAR FLIGHT HANDBOOK
(СПРАВОЧНИК ПО МЕЖЗВЕЗДНОМУ ПУТЕШЕСТВЮ)
Стр. 100
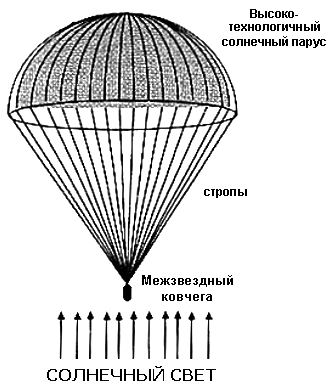
Рис. 6.2 Разгоняемый солнечным светом парусный межзвездный ковчег
|

...для более массивной полезной нагрузки, сосредоточенной в одном месте или для обитаемого модуля с людьми на борту, "ковчега", конфигурация паруса напоминает круглый парашют (смотри рисунок 6.2). Сеть строп чрезвычайно высокой прочности на разрыв должна идти от внешнего края паруса чтобы передать тягу буксируемой полезной нагрузке. Чтобы сохранить форму, полностью развернутый парус должен вращаться для уравновешивания внутренний радиальный компонент нагрузки в волокнах. Фактически, значительное количество энергии должна надежно сохранена в виде момента вращения большого выпуклого паруса.
|
|
Страница 100 из СПРАВОЧНИКА ПО МЕЖЗВЕЗДНОМУ ПУТЕШЕСТВИЮ (THE STAR FLIGHT HANDBOOK) Малова и Мэтлоффа. Взята на сайте Мэтлоффа gregmatloff.com.
|
3. АНАЛИЗ НАПРЯЖЕНИЙ В КОНСТРУКЦИИ
Рассматривая динамические напряжения в такой системе межзвездного привода, мы первым делом исследуем стропы (тросы). Мы обозначим, как показано на рисунке 4, длину троса Lc, радиус проекции паруса на Солнце (мидель), Rs , а Q - угол между нормалью к плоскости парусу и тросом ("Q" - читать "эта"). Самая высокая нагрузка возникает в тросах, присоединенных к внешнему периметру круглого паруса. Если TC - нагрузка на трос, то FS - составляющая нагрузки на трос, вызванная давлением света, а FR - радиальная составляющая нагрузки на парус, направленная к центру паруса.
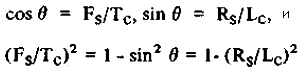 (13) (13)
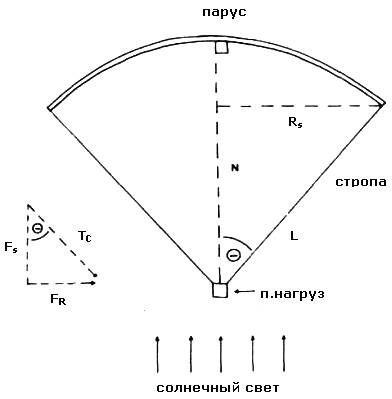
Рисунок 4. Схема нагрузки на парус и троса строп: L - длина строп, Q - угол между нормалью к плоскости паруса (N) и тросом, RS -эффективный радиус проекции паруса на Солнце (радиус миделя), TC - нагрузка на трос, FS - составляющая нагрузки на трос вызванная солнечным давлением на парус и FR - радиальная составляющая нагрузки на парус. Диаграмма сил и математические (физические не существующие) элементы конструкции показаны пунктиром.
Следует ожидать оптимальных значений параметров при условии (FS /TC)2 = 1/2, (RS/LS)2 = 1/2, которые получаются при (RS/LC) = 0,7, Q = 450, TC = 1,4FS, LC = 1,4R и FR = FS.
Присутствие радиальной составляющей силы на парусе приводит к появлению купола, который должен сбалансировать ее, если парус не очень жесткий. Некоторые детали проекта такой тросовой подвески будут еще рассмотрены далее. Плотность материала троса запишем как pC, ("p"- читать как"ро"), а предел прочности троса n ( "n" -читать как "ню"). Если общее сечение AC то пиковая нагрузка (сила) на тросы будет записана:
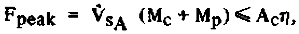 (14) (14)
Где V*sA - максимальное ускорение и, еще раз, MC общая масса тросов, а MP общая масса полезной нагрузки. Согласно уравнению (1) и вышеупомянутому предположению MC=pCLCAC=1,4pCRSAC. Если использовать алмазные тросы для определения верхнего предела прочности материалов, то плотность материала кабеля - pC = 3,52x103 кг/м3, а n = 5,3x1010 Н/м2 [14]. Тогда уравнение (14) можно перезаписать так:
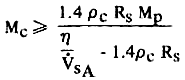 (15) (15)
что позволяет нам связать суммарную массу тросов с массой полезной нагрузки, максимальным ускорением корабля и радиусом паруса. Для массы кабелей:
MC >= MP , n/V*sA = 2,4pCRS ,
для MC>0,5MP, n/V*sA = 4,2pCRS,
для MC > 2,0MP , n/V*sA = 2,1pCRS.
Решение уравнения (15) для алмаза и меди (для меди pC = 8,52x103 кг/м3, n = 3,71х1010 Н/м2) [17] показано на рисунке 5, для ускорений 6 gearth и 10 gearth.
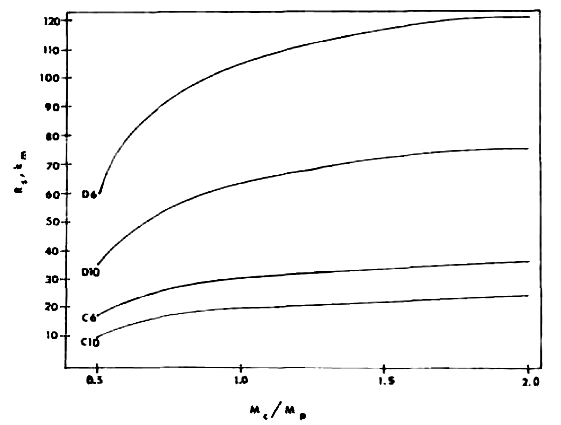
Рисунок 5. Эффективность степени раскрытия паруса для полностью натянутых кабелей, как функция от отношения массы кабеля к массе полезной нагрузки (MС/MP), материал кабеля (D - diamond, алмаз; C = copper, медь), для разных максимальных ускорений V*sA. Случаи D6 и D10 - алмаз для V*sA = 6 и 10 gearth соответственно. C6 и C10 - аналогично для меди.
Теперь мы рассмотрим FR, радиальную компоненту натяжения кабеля. Имеется два способа компенсировать эту составляющую тросовой нагрузки. Один способ требует, чтобы парус вращался, другой требует обеспечить наклон паруса внутрь, как показано на рисунке 6. Сначала рассмотрим вращающийся парус, в котором для компенсации FR, используется центробежная сила.
Для угла тросовой подвески паруса Q = 450, как показано на рисунке 4, где FR=FS, необходимая центробежная сила для балансировки радиальной нагрузки от тросов FR, возникает при линейной скорости вращение краев паруса VSPIN, значение которой можно вычислить так:
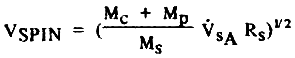 (16) (16)
Для случая MC = MP, MC + MP = MS, и V*sA = 104 см/c2 (~ 10 gearth). VSPIN~ (102RS)1/2. Для паруса радиусом 10 км VSPIN ~ 1 км/с и для паруса радиусом 100 км, VSPIN ~ 3 км/с.
Кинетическая энергия вращающегося парса записывается так [15]:
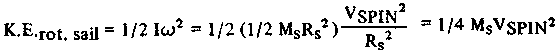 (17) (17)
где w ("w" - читать "омега") - угловая скорость вращения полотнища паруса. Для паруса радиусом в 100 км, минимальная масса паруса (без вращения) созданного из самого тонкого из возможных материалов, буде составлять ~ 4x105 кг. Таким образом, при линейной скорости вращения VSPIN = 3 км/с, K.E.rot.sail = 3x1012 Дж. Поэтому очень существенное количество энергии должно быть предварительно уже запасено в виде кинетической энергии вращения паруса, прежде чем тот покинет тень астероида.
Если вращение паруса после его полного разворачивания и завершения разгона солнечным давлением останавливать, то энергия вращения должна рассеиваться с мощностью 108-109 Ватт, а сам парус должен быть достаточно прочным, чтобы выдерживать уже неуравновешенное нагрузкой кабелей в свободном полете центробежную силу. Максимально возможная неуравновешенная радиальная нагрузка вдоль паруса может быть записана так:
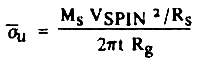 (18) (18)
где t - толщина паруса, а Rg = 0,7RS для круглого паруса [16]. Заменив MSVSPIN2/RS = MSV*sA, MS = pC t п RS2, где pC - плотность материала паруса и приняв Rg=0,7RS, мы получим
bu- = 0,7 RSV*sA. Для случая V*sA, = 102 м/с2, и RS = 105 м, bu- = 7x1010pS. Для алмазного паруса pS = 3,52x103 кг/м3 , и bu-=2,5x1010 Н/м2.
Таким образом, алмазный парус имеет приблизительно двойной запас по пределу прочности, но использование алмазных парусов увеличило бы минимальное значение bS до величины много большей чем 1,18 x 10-3 кг/м2.
Кроме того, как мы обсудим позже, нельзя избежать повреждения паруса от столкновения с микрометеоритами, по мере пересечения Солнечной системы. Такие столкновения могут очень значительно понизить в том или ином месте прочность быстро вращающегося полотнища. Альтернативой вращающемуся парусу должен стать наклоненный внутрь парус, как показано на рисунке 6.
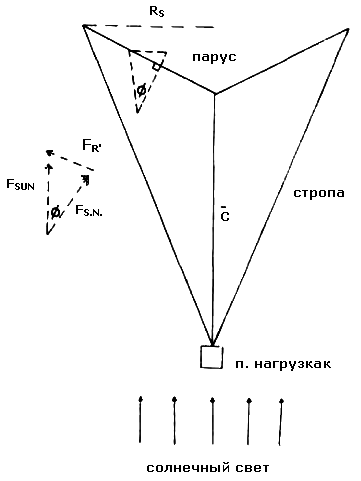
Рисунок 6. Использование наклоненного внутрь паруса для балансировки радиальной компоненты натяжения тросовой подвески. Угол Ф это угол между давлением солнечного излучения FSUN и компонентой нормали к парусу, FS.N. Центральный кабель C - соединяет полезную нагрузку с центром паруса. FR' - радиальная компонента давление солнечного света на парус.
На рисунке 6 угол Ф представляет собой угол между осью на Солнце и компонентой солнечного давления по нормали к парусу FS.N., в результате чего возникает вектор солнечного давления FR', который является радиальной компонентой направленные от центра паруса.
Если FS.N. и FR', находятся под углом Ф = 450 то площадь солнечного паруса (и следовательно его масса) увеличивается в два раза по сравнению с дисковым парусом той же эффективной проекции на Солнце RS. Хотя этот подход по массе более консервативен, чем вращающийся парус, оба они взаимно не исключают друг друга.
Кроме того, по мере того, как солнечный парус удаляется от Солнца пересекая Солнечную систему, плотность солнечного давления падает пропорционально r2, ускорение парусника падает, а значит и снижается напряженность в стропах и парусе b- . Соединяющая центр паруса с полезной нагрузкой стропа, поэтому, постепенно может удлиниться, что приведет к уменьшению угла Ф и "раскрытию" паруса.
Так как солнечный парус является тонкой пленкой, под однородным солнечным давлением, следует так же проанализировать влияние мембранного напряжения [17]. Если солнечное давление нормальное к парусу тогда FS.N. создает на нем RC - радиус искривления (рисунок 7) и, зная t- толщину мембраны (то есть материала паруса), мембранное напряжение может быть рассчитано так:
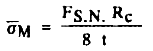 (19) (19)
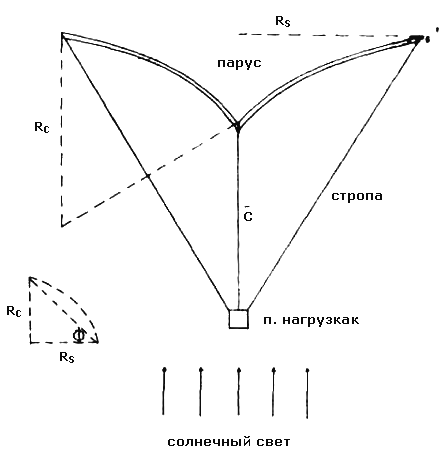
Рисунок 7. Окончательный вид частично развернутого паруса после учета мембранного эффекта. RС - радиус искривления паруса, t - толщина паруса. Все остальные параметры определены на рисунках выше по тексту.
Приняв предельный случай, что парус обладает 100% отражением, и в перигелии поток солнечного света нормален к поверхности паруса, уравнение (2) можно подставить в уравнение (19) и получить радиуса искривления под силой давления света Солнца:
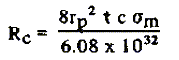 (20) (20)
Для rp = 1,5x109 м, t = 10-8 м, мы получили RC = 8,88x10-6bM. Алмазный парус n = 5,3x1010 Н/м2 имеет RC = 46,64 км. Медный парсу с n=3,71x1010 Н/м2 имеет RC = 32,94 км, и кремниевый парус с n~1010 Н/м2 имеет RC~9 км, для n = bM [14].
Используя максимальное искривление паруса на начальном этапе полета, мы уменьшаем, и мембранное напряжение, и перегрузку для команды. Полусферический парус имеет 1/2 ускорения от того же паруса, развернутого как плоскость. Угол Ф на рисунке 7 идентичен углу Ф на рисунке 6 (45 0), искривление паруса может уменьшаться по мере того, как корабль удаляется от перигелия, что позволить эффективной площади паруса увеличиться примерно в два раза. Таким образом, просто разворачивая парус и уменьшая его искривление в процессе удаления от Солнца, мы можем увеличить эффективную площадь паруса в четыре раза. Угол ? больший чем 450 по всей видимости тоже допустим. Так при угле в 550 эффективная площадь увеличивается в 6 раз по мере разворачивания паруса.
При такой конфигурации системы длина строп может быть больше чем оптимальное значение, вычисленное выше. Лишние части строп, которые возникнут по мере удаление корабля от Солнца, могут быть отброшены как балласт. Балласт в виде дополнительной длины тросов является еще одним фактором, смягчающим начальное ускорение.
Хотя плотность микрометеоритов у Солнца может быть значительно меньше, чем у Земли, следует позаботиться о микрометеорной защите паруса. Это особенно необходимо, в силу того, что заметное микрометеорное воздействие может сильно снизить в некоторых местах способность паруса выдерживать нагрузку.
Из осторожности, мы будем использовать консервативную оценку Лэя (Ley) для околоземного пространства которая предсказывает 2950 столкновений в час на 93 м2, с метеоритами размером около 5x10-7 м в поперечнике [18]. Много меньшие по размеру метеориты будут скорей всего уноситься солнечным ветром и вспышками далеко от Солнца. Бо'льшие по размеру встречаются значительно реже. Любой микрометеорит, оторвавшийся от кометы проходящий близко от Солнца, будет почти наверняка быстро испарен плотным электромагнитным потоком энергии от Солнца.
Мы полагаем, что сеть из волокон, расположенная на обратной стороне паруса (обращенной в космос) будет принимать на себя основную часть силовой нагрузки на солнечный парус. Если мы потребуем чтобы область паруса (внутри ячейки созданной несущей структурой) функционировала в среднем пять часов без столкновения с микрометеоритом, то такой фрагмент паруса будет иметь площадь 6,3x10-3 м2. Если мы имеем квадратную сетку, то потребуется расположить волокна с шагом 0,08 м друг от друга (Рисунок 8).
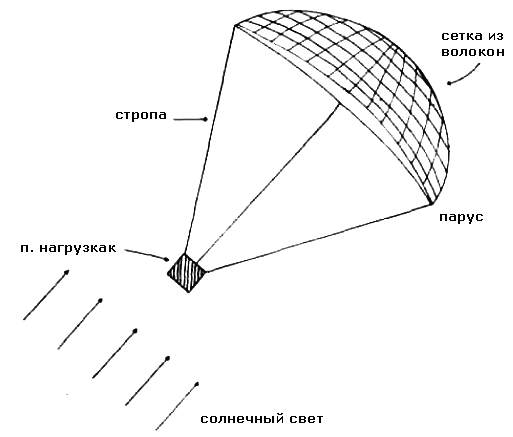
Рисунок 8. Сетка из волокон, принимающих нагрузку от полотнища и защищающая полностью развернутый парус от последствий столкновения с микрометеоритами.
Число волокон может быть записано как 50Rs (м) для шага между волокнами 0,08м, где Rs - радиус паруса в метрах. Если мы используем волокна наподобие тех, что предложил Форвард плотностью 2,0x10-3 кг/м3 и диаметром 10-5 м [19] и рисунок сетки волокон на тыльной стороне полностью развернутого паруса будет такой как показан на рисунке 8, то полная масса несущей сетки можно записать так:
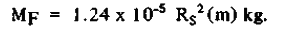 (21) (21)
Волокна добавляют менее 35% массы самого тонкого из технологически возможных парусов.
Возникает суммарно [25Rs (м)]2 штук элементов паруса. Поэтому парус радиусом 40 км имеет 1012 элементов. Если полная масса космического корабля 5x106кг и максимальное ускорение 25 gearth (обе величины явно завышены), то нагрузка на каждый элемент области будет 1,23x10-3 Н. Если мы допустим, что вся нагрузка, которая возникает на данном сегменте паруса выдерживается одним смежным волокном, то нагрузка на волокно вызванное указанным ускорением космического корабля будет 1,54x103 Н/м2. Так как волокна Форварда могут выдерживать нагрузку на разрыв в 3x108 Н/м2, мы обеспечены запасом прочности на несколько порядков и можем не волноваться [19].
Предполагая же (в противоположность вышесказанному) что вся нагрузка внутри области охваченной волокнами, должна быть принята всеми волокнами элемента, то нагрузка на парус будет 0,2 Н/м2 что является в пределах уже сейчас изготавливаемых коммерческим способом тонких пластиковых пленок, не говоря уже о более прочных произведенных в космосе солнечных парусов для которых здесь было принято что их предел прочности от 1010 до 5,3x1010 Н/м2.
Таким образом, проблемы силовых нагрузок не выглядят непреодолимой, хотя забота о них несколько снижают эффективность реального паруса по сравнению с идеальным. Далее мы рассмотрим различные дополнительные аспекты миссии и стратегию разворачивания паруса.
4. ПРЕДВАРИТЕЛЬНЫЙ ПРОЕКТ МИССИИ
И СТРАТЕГИЯ РАЗВОРАЧИВАНИЯ ПАРУСА
Враждебность тепловой нагрузки на расстоянии 0,01 а.е. от центра Солнца, серьезный вызов проектировщикам системы. Плоский парус на расстоянии 0,01 а.е. от Солнца получит 1x107 Вт/м2. Полагая, что обе стороны паруса будут поглощать и излучать как абсолютно черное тело, получаем, что парус будет нагрет до температуры 31000K. Если же 90% света им будет отражено, то температура паруса в перигелии составит 17500 K. Парус с отражательной способностью 95% и 99% будет иметь в перигелии соответственно 15000К и 11000 K [20]. Отражающее покрытие паруса с зеркальностью 95% или больше не кажется чем-то недостижимым [21]. Изогнутый, вывернутый наружу парус получить меньший поток по нормали к своей плоскости и, следовательно, будет иметь в перигелии температуру еще ниже. Если в перигелии парус с зеркальностью 95% повернут так, что он получает только 25% потока от нормального, то температура паруса будет ниже 11000K, а аналогично расположенный парус с зеркальностью в 99% будет иметь температуру ниже 8000К.
Металлические паруса будут использовать температурный диапазон 1000 0-2000 0K. Бор имеет точку плавления 26000K и плотность 2,5x103 кг/м3, поэтому парус из бора толщиной 10-8 м имел бы 2,1 раза большую массу, чем самые тонкие из проектируемых парусов [22]. Возможно, что, в конечном итоге, можно будет приблизиться к окончательному решению по дизайну паруса, используя сверхпрочные волокна, но такие современные волокна, кажется, не годятся для температур более 10000K [23].
К счастью продолжительность тепловой нагрузки в перигелии будет невелика. Так самый медленный вариант в Таблице 1 проходит точку перигелия в 0,01 а.е. и уходит в космос со скоростью 0,0014с (420 км/с). После 0,5 часа ускорения корабль будет приблизительно в 2,3x106 км от центра Солнца. И поток солнечного излучения (и ускорение) упадут до 44% от пикового значения. Температура паруса с зеркальностью 90% и ориентированному перпендикулярно потоку, упадет до to 14500K.
Скорость прохода перигелия одновременно является и преимуществом и проблемой. Преимущество в том, что в большинстве случаев продолжительность теплового удара буде длиться приблизительно столько же, сколько длиться тепловая нагрузка в атмосфере на спускаемый аппарат при возвращении с орбиты. Абляционный экран, используемый для современных спускаемых аппаратов, может быть адекватно использован и здесь для защиты полезной нагрузки.
Проблема же, вызванная скоротечностью прохода перигелия - это разворачивание паруса. Нет никакого очевидного способа развернуть парус радиусом 1-200 км и с поверхностной плотностью 1,18x10-5 - 1,18 x 10-4 кг/м2 в течение минут или даже секунд. Так в случае прохода перигелия по траектории с 0,0014с конечной скоростью (самая простая) одноминутная ошибка в разворачивании паруса составит 25 000 км, что составляет угловую ошибку в 0,10. Для путешествия на расстояние в 4-е световых года это составит промах на 441 а.е., если потом в середине полета не проводить корректировку курса.
Один способ облегчить эту проблему - обеспечить корабль "стартовое прикрытие", мертвый кусок материи (обломок скалы, с которого запускается мобильная колония) и который много массивней чем сам корабль и парус. Поперечное сечение обломка должно быть как у предварительно развернутого паруса, а так же он должен иметь низкое альбедо. Как показано на рисунке 2. В перигелии звездолет совершил бы отделение от своего стартового прикрытия, который продолжит полет (в случае гравитационного маневра у Сатурна) по около-параболической траектории вокруг Солнца. В принципе, такие астероидные обломки могли бы быть сами оборудованы самостоятельными парусами для совершения орбитальных маневров и несли бы двойное назначение, обеспечивая дополнительную тепловую защиту для звездолета по мере приближения того к перигелию. Малая часть массы щита или стартового прикрытия может быть изготовлена в виде солнечного паруса без полезной нагрузки. Такой "зонд" может быть запущен перед основным звездолетом, чтобы подмести метеоритный обломки на его пути и таким образом уменьшить вероятность разрушения солнечного паруса звездолета. Но как обсуждалось выше, высокая тепловая активность вблизи перигелия может значительно снизить потребность в подобной операции.
Если солнечный парус звездолета развернуть в перигелии так, что максимальное ускорение судна составит 6gearth, то темная, не отражающая астероидная масса в 5 раз большая, чем масса судна подверглась бы ускорению 0,6gearth до момента освобождения паруса. Конечная скорость судна уменьшилась бы меньше чем на 5% за счет обратного давления на теневой щит на подлете. Это влияние можно было бы компенсировать, запустив теневой щит чуть ближе, чем перигелий или используя более массивный обломок астероида.
В случае маневра у Сатурна, который бы увеличил скорость в перигелии до 0,002 c, теневой щит покинет Солнечную систему. При скорости в перигелии 0,0014c астероид останется в Солнечной системе и может быть использован для других миссий.
После того как теневой щит отброшен, и звездолет с солнечным парусом начинает удаляться от Солнца световой поток начнет падать и площадь паруса, нормальная к Солнцу может быть увеличена. В большинстве миссий звездолет будет удаляться от перигелия так, что эффективный радиус паруса должен увеличивается на десятки километров в час. Развертывание паруса с такой скоростью, как видится, не представляет непреодолимых проблем.
Интенсивная магнитная (и неэлектромагнитная) радиация в окрестностях Солнца так же будет представлять собой проблему. Так как ни один зонд с Земли не выполнил успешного пролета вплотную у поверхности Солнца, наши знания о внешней короне светила очень скудные [24]. Межпланетное магнитное поле обычно имеет напряженность 10-9 Вебер/м2 на расстоянии 1 а.е [24]. Если солнечное магнитное поле упрощенно представить как диполь, то напряженность поля на 0,01 а.е. будет 10-3 Вебер/м2 что в 20-30 раз сильней чем напряженность поля на поверхности Земли. Термически защищенный сверхпроводящий магнит обеспечил бы защиту от солнечного магнитного поля, если бы необходимость этого была доказана.
Таблица 2. Распределение массы полезной нагрузки для межзвездной колонии на 1 000 человек.
| Торроидальная структура (1000 человек по 35 м2/человека) |
2,5x106кг |
| Атмосфера |
106кг |
| Электростанция, оборудование, инструменты |
~2,0x106кг |
| ИТОГО |
~5,5 x106кг |
В таблице 2 приведена масса конструкции, атмосферы, генерирующей энергию системы, прочего оборудования и инструментов на 1000 человек (35 м2/чел.) [25]. Если снаряжение подбирается для колонизации планетной системы, масса полезной нагрузки в 107 кг выглядит реалистично.
Для определения параметров простейшей миссии сначала рассмотрим парус с поверхностной плотностью (включая сетку силовых волокон) bS - 5x10-5 кг/м2 и Rs = 50 км. Масса паруса составит тогда 3,93x105 кг. Мы принимаем MS = MC + MP и MC = 2MP. Используя уравнение (15) для алмазных тросов получаем V*sA = 14,6gearth и для медных тросов V*sA = 4,2gearth. Из рисунка 3 для ускорения в 14g и без маневра у Сатурна время полета к Альфа Центавра составит 1000 лет. С маневром у Сатурна полет продлиться 950 лет. Для предельного ускорения в 4gearth потребуется 1350 и 1200 лет (экспедиция к Альфе Центавра) если не делается маневр у Сатурна и если такой маневр выполняется, соответственно. Так как полезная нагрузка каждого солнечного паруса 1,3x105 кг, то потребуется в итоге 42 таких солнечных паруса для мисси с полезной нагрузкой в 5,5x106кг и 76 солнечных паруса для мисси массой 107 кг.
Чтобы уменьшить число отдельных солнечных парусных звездолетов и соответственную сложность запуска такой экспедиции, рассмотрим максимальное увеличение радиуса солнечного паруса до Rs =100 км. Потребуется 10 парусов для полезной нагрузки в 5,5x106
кг для полета до Альфы Центавры и максимальное ускорение для алмазных тросов составит 7gearth. Без маневра у Сатурна время путешествия к Альфа Центавра составит приблизительно 1200 лет, с маневром у Сатурна - около 1100 лет.
Если Rs увеличить до 190 км и использовать алмазную тросовую подвеску, то максимальное ускорение может составить 4gearth и понадобится только 3 парусника чтобы отправить 5,5x106 кг полезной нагрузки, которая долетит до Альфы Центавры приблизительно через 1350 лет без маневра у Сатурна. С маневром - за 1200. Население межзвездной колонии в 1000 человек, конечно же, выбрано несколько произвольно.
Уравнения (11), (12) и (5), а так же рисунок 3 могут использоваться для оценки влияния на результат, если уменьшить ?e. Если be понизить от 10-4 до 3,73x10-5 кг/м2 , приняв Ms=Mc + Mp и Mc = 2Mp как в случае, обсуждавшемся выше, парус радиусом 190 км с ускорением 4gearth потребует меньше чем 950 лет для полета к Альфа Центавра с маневром у Сатурна и 1000 лет без какого либо транзитного маневра. Потребуется 8 солнечных парусников, чтобы запустить миссию 5,5x106 кг полезной нагрузки.
Детали траектории солнечного межзвездного парусника после прохождения им перигелия могут быть исследованы с использованием аппроксимирующих кинематических уравнений:
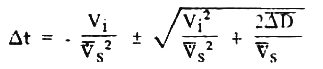 (22) (22)
где dt - время необходимое звездолету чтобы пересечь приращение расстояния dD ("d"- читать как "дельта"). Vi - скорость в начале пересечения дистанции dD, V*-s - среднее ускорение в пределах dD.
Хорошая аппроксимация деталей может быть получена, если выбирать малые dD, в пределах которого вычисленное световое давление от Солнца и гравитационного ускорения следует считать одинаковым на обоих концах dD. Изменение скорости с каждым dD, dV, должно быть аппроксимировано как dV ~ Vsdt, которое позволяет нам получить Vi для следующего приращения расстояния.
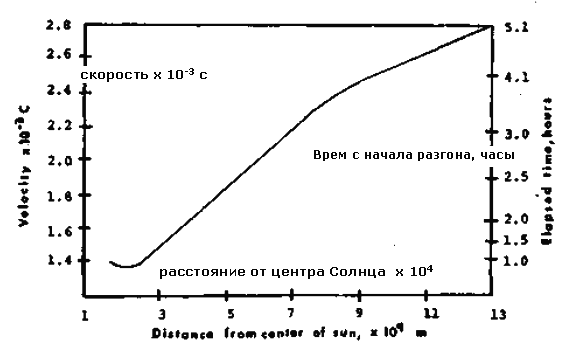
Рисунок 9. Аппроксимация траектории звездолета на солнечных парусах с параметрами: Rs = 190 км, V*sA = 4gearth, M = 1,13x107 кг, рефлективность паруса =1. Судно начинает ускорение в перигелии (1,5x109m) с начальной скоростью 0,0014c. В начале происходит небольшое падение скорости, потому что в самом начале полета гравитационное ускорение от притяжения Солнца больше ускорения от солнечного давления. Парус полностью разворачивается, и вся балластная масса сброшена через 3,1 часа после прохода перигелия.
Рисунок 9 представляет детали кинематики самого медленного звездолета, из обсуждавшихся выше с Rs = 190 км, V*sA = 4gearth, M = 1,13x107 кг, M = 1,13x107 кг, r0= 1,5 x109 м,V0 = 0,0014c и рефлективностью паруса 1,00. Хотя основная часть ускорения звездолета происходит в течение первых 5-и часов, для оптимизации разгона, возможно следует увеличить долю массы паруса за счет уменьшения массы строповых тросов и таким образом уменьшить деградацию паруса от микрометеоритов. Если массу силовых волокон увеличить до 33% от общей массы паруса, то парус увеличит живучесть в половину в 10 часов и поверхностная плотность паруса составит 3,35x10-5 кг/м2.
Удачно, что полезная нагрузка является только небольшой частью (в данном случае 20%) от полной массы покидающей перигелий. Парус и такелаж должны быть сохранены во время полета в открытом космосе и размещены (свернуты) вокруг полезной нагрузки для защиты ее от межзвездной радиации.
В перигелии 0,01 a.e., полностью развернутый парус с be ~1,2x10-4 кг/м2 ускоряется с 76 gearth (Таблица 1). Для того чтобы уменьшить ускорение до 13 gearth, парус искривляется, и его наклон можно было бы увеличить балластной массой концентрически расположенной вокруг полезной нагрузки, присоединив к такелажу паруса. Эта масса могла бы выполнять двойную функцию как экран от солнечной радиации во время прохода перигелия и постепенно сбрасывалась бы вместе с освободившимся такелажем по мере ускорения и удаления корабля от Солнца.
В случае многопарусной конструкции солнечные паруса могли бы быть связаны в конфигурацию "ожерелье" или "косичка". Как альтернатива, может использоваться некоторый вспомогательный привод для маневра и встречи отдельно запущенных парусников после завершения разгона.
В качестве вспомогательного привода для коррекции курса, стыковки модулей и дополнительного разгона в процессе движения по траектории отбытия, может быть использована относительно скромная технология типа электроракеты на солнечных батареях или ускоритель массы [26]. Первая корректировка (10-и минутной ошибки с раскрытием паруса) составит приращение скорости ~0,02v, это около 25 км/с.
5. МЕЖЗВЕЗДНЫЙ ПОЛЕТ И ТОРМОЖЕНИЕ
Кинетическая энергия большого звездолета, даже если он движется с относительно скромной по межзвездным меркам скоростью, огромна. Судно массой в 5x107 кг движущееся со скоростями 0,003с или 0,004с имеет 2,03x1019 или 3,6x1019 Джоулей кинетической энергии соответственно. Энергии самого медленного из этих кораблей, достаточна чтобы получать 5x108 Ватт энергии для нужд команды, непрерывно в течении 1300 лет путешествия. Если начальная скорость уменьшится за счет этого только на 7% за весь срок межзвездного круиза, и если она превращается в электроэнергию с 15%-й эффективностью, то для нужд команды доступна постоянная мощность 107 Ватт. Таким образом, население в 1000 человек могло бы поддерживаться энергией в 10 кВт на каждого человека. Солнечный свет, фокусируемый на судно солнечным парусом с эффективным радиусом в 350 км, мог бы обеспечить такую энерговооруженность (с 30% эффективностью конвертирования) только до 4000 а.е. от Солнца (0,06 световых лет).
Возможные методы получения на борту энергии от кинетической энергии судна были описаны в ссылках [15] и [22].
Также как и для получения энергии, для корректировки курса в середине траектории полета можно использовать сверхпроводящий магнитный коллектора и борановый парус [22]. Регулируя угол паруса покрытого бором как показано на рис. 10, с помощью подобного коллектора и паруса становится возможным корректировка курса на несколько градусов за счет потери 10% от первоначальной скорости полета корабля,.
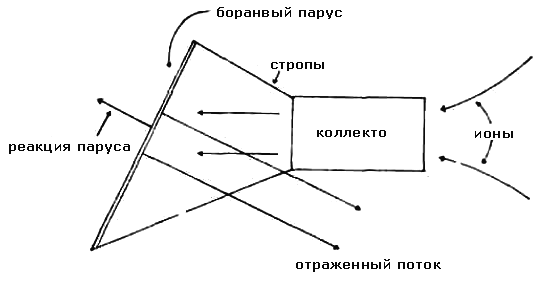
Рисунок 10. Корректировка курса в середине пути с использованием магнитного коллектора и тормозного паруса из боранов.
Большая часть процедуры торможения у цели происходит в два этапа. Сначала за несколько десятых светового года от системы назначения, начинают использовать электростатический парус, чтобы замедлить космический корабль до скорости < 0,001c. Для окончательного торможения частично разворачивается уже солнечный парус. Потому что столкновение ионов с электростатическим парусом согласно [27] будет упругим, и радиус поля ~ 3x105 км является разумным, торможение таким парусом на 0,003с может происходить с ускорением 0,7 м/с2. На скорости 0,001c, ускорение составит 0,08 м/с2. Сам же солнечный парус должен использоваться только на самой заключительной стадии торможения и для маневрирования в пределах планетной системы звезды-цели.
6. ЗАКЛЮЧЕНИЕ
Перспектива в ближайшем будущем запустить высокотехнологичный межзвездный зон на солнечном парусе со скоростью выше 0,01с очень интригующая. Хотя максимальная скорость для робота-зонда на солнечном парусе меньше чем 10% от максимальной скорости, на которой рассчитывает аналогичный зон на термоядерном синтезе, стоимость зонда на солнечных парусах, по всей видимости, окажется на много порядков ниже. Перспектива запуска такого типа зондов ниже обсуждается в нашем приложении, в работе Джэфф (Jaffe) и у других [28]. Они рассчитывают, что температура в перигелии может быть на 20% выше, чем мы здесь приняли, потому что излучающая способность тонкой фольга толщиной в 0,5 может быть выше, чем у фольги толщиной 1,0, принятой нами.
Требования безотказности работы систем солнечного парусника в процессе полета длиной в столетия повышают требования к автоматике зонда и делают их более строгими, чем в случае для полета термоядерного зонда длинной в десятилетия. Но сам запуск парусника мог бы оказаться менее проблематичной процедурой и более надежной, чем с помощью термоядерного синтеза.
Рассматривая более долгосрочные перспективы этой работы, следует отметить, что идея путешествовать тысячелетия на солнечно-парусной обитаемой колонии не выглядит привлекательной для землян. Однако, длительно живущие в "стационарных" космических обиталищах представители других цивилизаций Галактики не будут ощущать подобных ограничений. Кроме того, как указал Кармер (Kumar) в [29], эти расы могут иметь в своей окрестности ближайшие звезды куда ближе чем мы имеем Альфу Центавру, поэтому их колонии запускаемые солнечным парусом могут достигать цели за несколько столетий.
Многие аспекты разгоняемого солнечным парусом звездолета все еще остаются открытыми. Например, выбор привода для маневра у Сатурна (если в таком есть необходимость) или оценка дополнительного разгона на подлете к Солнцу (после маневра у Сатурна). Разгон можно было бы продолжить для сокращения времени путешествия, используя привод на потоке шариков материи Сингера (Singer) [30]. Быстро ускоряющиеся солнечные паруса могли бы разгонять поток шариков материи со скоростью в 0,01с и этот поток мог бы взрываясь, разгонять колонию, теряющую ускорение по мере удаления от Солнца.
Однако ясно: для случая межзвездного путешествия на солнечном парусе, даже в простейшем, неоптимизированном случае, можно сказать, что тысячелетняя миссия к звездам может быть запущена без того, чтобы разрушить экономику того, кто задумал организовать подобное мероприятие. Следующий шаг развития идеи - уделить внимание социологической проблеме поддержания существования между звездами нескольких дюжин или сотен людей в течение многих поколений, внимательно изучить технологические проблемы, типа, поиск лучшего способа извлечения и использования энергии в межзвездном пространстве, а так же изучить вопрос поддержания долговременной замкнутой экосистемы.
* * * * * * *

Через четыре или пять миллиардов лет, когда Солнце покинет главную последовательность, и Солнечная система станет менее гостеприимной для людей, наше светило постепенно превратится в лучший источник для плаванья под давлением звездного света. Согласно Новатни (Novotny) [31], Солнце в некоторый момент перехода в стадию красного гиганта будет иметь фотосферу, простирающуюся на 1 a.e., и его яркость увеличится тысячекратно.
Если мы возьмем "состояние искусства" солнечных парусов Тсу (Tsu) и расширим это для пилотируемой парусной колонии массой в 5x108 кг, то при плотности 2x10-3 кг/м2 масса паруса составит 4x108 кг и его диаметр составит 500 км [9]. Пиковое ускорение будет нежным (~ 0,5 g) и Vinf~ 0,004с, если стартовать с круговой орбиты в 1 а.е. А максимально оптимизированная колония на солнечном парусе должна быть способна покинуть систему красного гиганта со скоростью ~ 0,01с.
Ясно, что метод разгона межзвездного зонда солнечным светом должен серьезно изучаться в оставшиеся десятилетия этого тысячелетия как наиболее реальная идея подобного рода. Но может случится, что и в отдаленном будущем, даже если наши потомки будут прогрессировать и освоят более быстрые методы межзвездного путешествия, именно разгоняемые солнечным светом парусники могут оказаться спасительным средством для древней цивилизации Солнечной системы когда наше светило постигнет катастрофа превращения в красного гиганта.
БЛАГОДАРНОСТИ
Г. Мэтлофф крайне благодарен Эрику Дрекслеру (Eric Drexler) за обсуждение концепции высокоэффективных солнечных парусов в мае 1979-го во время конференции по Космическому производству в Принстоне. Г. Мэтлофф, также, высоко оценил беседу с профессором М. Маутнером (M. Mautner) из университета Рокфеллера (Rockfeller University). Численный анализ были проделаны на оборудовании Техасского института, SR52 программируемый калькулятор.
ПРИЛОЖЕНИЕ:
РОБОТИЗИРОВАННЫЙ МЕЖЗВЕЗДНЫЙ ЗОНД НА СОЛНЕЧНОМ ПАРУСЕ
Хотя главные усилия авторов данной работы были направлены на пилотируемый звездолет, запускаемый солнечным парусом, более реалистичное применение данной технологии могло бы начаться с запуска легкого роботизированного межзвездного зонда. Он мог бы быть либо уменьшенной версией межзвездного пилотируемого звездолета, с полезной нагрузкой подвешенной на стропах развернутого к солнцу паруса, или быть аппаратом, полезная нагрузка которого распределена в виде тонкой пленки на теневой стороне паруса.
В любом случае, так как миссия не лимитируется жесткими требованиями по ограничению пикового ускорения, то может быть достигнута несколько большая конечная скорость, чем в случае пилотируемой мисси. Маневр у Сатурна, как обозначено в уравнении (5) является достаточно несущественным для высокого Vinf. Небольшой зонд, скорей всего, мог бы стартовать непосредственно с орбиты Земли, обходясь только этим маневром.
Типичная миссия межзвездного зонда с солнечным парусом могла бы происходить следующим образом. Парус/полезная нагрузка имеют плотность be = 2x10-5 кг/м2 и Rs = 103 м и могут быть развернуты на околоземной орбите. Полная масса зонда могла бы составить 63 кг и если зонд отправляется с орбиты Земли на почти параболическую орбиту Солнца с V0 = 0,001с, то он уйдет от Солнца с максимальным ускорением 439gearth и достигнет Vinf = 0,012с. Тогда полет до Альфа Центавра занял бы приблизительно 350 лет.
В течение длительного межзвездного полета 10 кг полезной нагрузки (или около того) могли бы использоваться для исследования межзвездной среды. Тонкая оптическая структура может быть нанесена на многокомпонентный парус. Недавно было сделано предложение, что межзвездные зонды, покидающие Солнечную систему, могут использовать гравитационное поле Солнца как усилитель (радиолинзу) радиоизлучения от других звезд, неслышного вблизи Солнца и таким образом действовать как SETI детекторы [32].
Чтобы зонд извлекал энергию из межзвездной среды, можно применить межзвездную версию межпланетной машины Алфвена (Alfven) [33] или использоваться лист сверхпроводника, типа недавно предложенного Метлоффом и Фенелли (Matloff, Fennelly) [22]. Оба эти подхода в конечном итоге привели бы к некоторому торможению корабля, поэтому тонкопленочная радиоизотопная батарея все еще может рассматриваться как альтернатива.
Перед уходом из Солнечной системы зонд должен двигаться в тени намного более массивного щита подобных ему размеров. Для темного (возможно аблятивного) щита/паруса ускорение может быть ограничено 0,44gearth если масса щита составляет 3,2x104 кг, что является в пределах существующих транспортных систем, особенно если внешний топливный бак челнока может быть оставлен на орбите и использован для формирования тела щита. Таким образом, еще в XX столетии мы можем разработать тонкопленочный межзвездный зонд, разгоняемый солнечным парусом, которому потребуется несколько столетий для того чтобы достигнуть Альфа Центавра.
СПЕЦИФИКАЦИЯ
AC = суммарная площадь сечения всех тросов стропы.
c = скорость света, 3x108 м/с
С = трос-стропа соединяющая полезную нагрузку с центром солнечного паруса.
FR = радиальная сила на парус, вызванная натяжением строп.
FR' = радиальная компонента солнечного давления на парус
FS = компонента нагрузки в кабеле, компенсирующая радиальное давление солнечного света
FS.N. = компонента солнечное давление нормальная к поверхности солнечного паруса
Fsun = давление солнечного света.
gearth = ускорение свободного падения 9,8 м/с2
G = Гравитационная постоянная 6,668x10-11 Н*м2/кг2
I = момент инерции вращения солнечного паруса
К.Е.rot sail = кинетическая энергия вращения солнечного паруса
LC = длина кабелей (основных строп)
M = общая масса паруса, его структурной сетки, строп и полезной нагрузки
MC = общая масса строп
Mp = общая масса структурной сетки паруса
MP = масса полезной нагрузки
Ms = масса отражающей поверхности паруса
M0 = Масса Солнца, 1,989x1030 кг
r = расстояние от центра Солнца
r0 = расстояние от центра Солнца в момент полного открытия паруса
rp = дистанция до центра Солнца в перигелии
RC = радиус искривления солнечного паруса
Rg = радиус вращения для солнечного паруса напряженного вращением
RS = радиус эффективной проекции паруса к Солнцу (радиус миделя)
RsF.S. = эффективны радиус для полностью раскрытого солнечного паруса
Sr = солнечная постоянна на расстоянии r, в Ватт/м2
t = толщина паруса, м
Tc = нагрузка в стропах
V0 = скорость судна в момент полного раскрытия паруса.
VCIRC = скорость, необходимая для поддержания круговой орбиты, на расстоянии rp
Vi = скорость на шаге в интервал времени dt при численном моделировании траектории
Vp = скорость в перигелии
Vspin = линейная скорость края вращающегося паруса
Vinf = скорость отлета парусника из Солнечной системы.
V* = ускорение
V*A = максимальное ускорение
Vs = средняя скорость на интервале времени dt при численном моделировании
dD = расстояние пройденное парусом за время dt при численном моделировании
dt = время начального ускорения после прохождения перигелия
n ("ню")=предел прочности строп, Н/м2
Q ("эта") = Угол между стропой и нормалью к парусу
k = отражающая способность паруса
pc ("ро-це") =плотность материала троса-стропы, кг/м3
ps = плотность материала солнечного паруса
be = эффективная масса корабля на толщину или поверхностная плотность, кг/м2
bpa = Поверхностная плотность тонкопленочного зонда.
bs = поверхностная плотность солнечного паруса
bpm = напряжение в мембране солнечного паруса
bu = максимальное несбалансированное радиальное напряжение вдоль вращающегося солнечного паруса.
Ф - угло между направлением на Солнце и FS.N.
w ("омега")= угловая скорость вращающегося солнечного паруса, рад/с
REFERENCES
1. T. C. Tsu, "Interplanetary Travel by Solar Sail," ARS Journal, 29, 422-427 (1959).
2. L. D. Friedman, W. Carroll, R. Goldstein, H. Harstead, R. Jacobson, J. Kievat, R. Landel, W. Layman, E. Marsh, R. Plosza, J. Stevens, L. Stimpson, M. Trubert, G. Varsi, J. Wright, J. Hedgepath and R. MacNeal, "Solar Sailing -The Concept Made Realistic," AIAA Paper No 78-82, (1978).
3. К. Е. Drexler, "High Performance Solar Sails and Related Reflecting Devices," AIAA Paper No. 79-1418; "High-Performance Solar Sail Concept," L-5 News, 4, No. 5, 7-9 (May 1979).
4. G. Marx, "Interstellar Vehicle Propelled by Terrestrial Laser Beam," Nature, 211, 22-23 (1966).
5. P. Norem, "Interstellar Travel, A Round-Trip Propulsion System with Relativistic Velocity Capabilities," AAS Paper No. 69-388(1969).
6. R. L. Forward, "Infrastellar and Interstellar Exploration," Hughes Research Report 503, September 1976.
7. D. R. J. Viewing, С J. Horswell and E. W. Palmer, "Detection of Starships, JBIS, 30, 99-104 (1977).
8. G. K. O'Neill, "The Colonization of Space," Physics Today, 27, No. 9, 32-40(1974).
9. G. L. Matloff and M. Mautner, "Solar Sails and Red Giants: The Final Fate of a Type II Civilization," presented at the 154th meeting of the American Astronomical Society, Wellesley, Mass., 11-14 June 1979, abstract in Bulletin of the American Astronomical Society, 11, No. 2,456 (1979).
10. I. S. Shlovskii and C. Sagan, Intelligent Life in the Universe, Holden-Day, San Francisco (1966).
11. K. A. Ehricke, "Saturn-Jupiter Rebound: A Method of High Speed Spacecraft Ejection from the Solar System," JBIS, 25,561-571 (1972).
12. M. R. Sharpe, Living in Space, Doubleday, Garden City, New York (1969).
13. R. W. Bucheim, Space Handbook: Astronautics and its Applications, Random House, New York (1959), pp. 138-141.
14. A. R. Martin, "Structural Limitations on Interstellar Spaceflight," Astronautica Acta, 16, 353-357 (1971).
15. A. L. Reimann, Physics - Volume I, Barnes and Noble, New York (1971) Chapt. 7.
16. G. R. Fowles, Analytical Mechanics, Holt, Rineholt, and Winston, New York (1962), Chapt. 8.
17. Sir R. Glazebrook, (ed.), Dictionary of Applied Physics -Vol. 1. Mechanics, Engineering and Heat, Peter Smith, New York (1950), p. 832.
18. W. Ley, Rockets, Missiles and Men in Space, Viking, New York (1968), pp. 517-518.
19. R. L. Forward, "Zero Thrust Velocity Vector Control for Interstellar Probes: Lorentz Force Navigation and Circling," AIAA Journal, 2, 885-889 (1964).
20. Calculations performed with a GEN-15C Radiation Calculator, as described by W. L. Wolfe, Handbook of Military Infrared Technology, Office of Naval Research, Dept. of the Navy, Washington, D. С (1965). Chapt. 2.
21. W. J. Smith, Modern Optical Engineering, McGraw-Hill, New York (1966), pp. 175-177.
22. G. L. Matloff and A. J. Fennelly, "A Superconducting Ion Scoop and Its Application to Interstellar Flight," JBIS, 27, 663-673 (1974).
23. J. H. Ross, "Superstrength-Fiber Applications," Astronautics and Aeronautics, 15, No. 12, 44-50 (1977).
24. J. С Brandt and P. W. Hodge, Solar System Astrophysics, McGraw-Hill, New York (1964), Chapt. 6.
25. R. D. Johnson (ed.), "Space Settlements, A Design Study," NASA SP-413, Scientific and Technical Information Service, NASA, Washington, D. С (1977), pp. 46-47.
26. G. K. O'Neill, "The Low (Profiles) Road to Space Manufacturing," Astronautics and Aeronautics, 16, No. 3, 24-33, (1978).
27. G. L. Matloff and A. J. Fennelly, "Interstellar Applications and Limitations of Several Electrostatic/Electromagnetic Ion Collection Techniques," JBIS, 30,213-222 (1977).
28. L. D. Jaffe, С Ivie, J. С Lewis, R. Lipes, H. N. Norton,
J. W. Stearns, L. D. Stimpson and P. Weissman, "An Interstellar Precursor Mission," JBIS, 33, 3-26 (1980).
29. S. S. Kumar, "Hidden Mass in the Solar Neighbourhood" Astrophysics and Space Science, 17,2194-222 (1972).
30. С E.-Singer, "Interstellar Propulsion Using a Pellet Stream for Momentum Transfer," JBIS, 33,107-115 (1980).
31. E. Novotny, Introduction to Stellar Atmospheres and Interiors, Oxford, New York (1973), Chapt. 7.
32. V. R. Eshleman, "Gravitational Lens of the Sun: Its Potential for Observations and Communications over Interstellar Distances," Science, 205,1133-1135 (1979).
33. H. Alfve'n, "Spacecraft Propulsion'. New Methods," Science, 176,167-168 (1972); also see С P. Sonett, V. Fahleson^md H. Alfve'n, "Electrodynamic Sailing: Beating into the Solar Wind," Science, 178,1115-1119 (1972).
Перевод Александр Семенов сентябрь 2009г, макет html май, 2011
Первоисточник.
Особая благодарность Ивану Моисееву за предоставление первоисточника.
ВРЕЗКА 3 от "Горизонта возможного"

|
У меня нет пока полной версии THE STAR FLIGHT HANDBOOK. Однако я могу вам предложить более позднюю и на этот раз полную версию книги Грегори Мэтлоффа аналогичного содержания гуляющую в Сети:
Gregory L. Matloff
Deep-Space Probes
To the Outer Solar System and Beyond
(Second Edition)
Зонд в глубокий космос
К границам Солнечной системы и дальше
(вторая редакция)
234 c. 3,83 МБ
Книга содержит систематический анализ всех концепций приводов для межзвездных путешествий. В приложении есть детальный разбор идеи межзвездных парусов.
|
|
Если вас интересует фантастическая литература, где разгоняемый солнечным светом парус-колония отправляется в тысячелетнее межзвездное путешествие, то в первую очередь вас должна заинтересовать книга культового французского писателя Бернарда Вербера написанная им в 2006 г. - "Звездная бабочка". Есть русский перевод, но ссылку не даю. Легко ищется в Сети по ключу.
Бернард Вербер
Звездная бабочка
2006 г.
англ. : "The Butterfly of the Stars"
Автор явно опирается на идеи Малова и Мэтлова. Но, придумывая парусный ковчег для своего романа, писатель упустил массу деталей и допускает ряд серьезных технических ошибок (легко заметных читателю данной статьи) и даже очаровательных чисто физических ляпов.
|

|

Так же следует признать достаточно утопичный социальный "месседж" романа. И, тем не менее, надо отдать Верберу, как писателю, должное. Любой роман этого француза сам по себе оригинальное явление. И этот - не исключение. На фоне же однообразного коосмооперного засилья в литературе, "Звездную бабочку" вообще можно достаточно уверенно отнести к твердой научной фантастике.
На фото слева Бернард Вербер с искуственной биосферой :)
__________________________________________________
[ вверх ] [ оглавление ]

Оптимизирован под Internet Explorer 1024X768
средний размер шрифта
Дизайн A Semenov
|